Spočítejte si: Kolik tepla vysálá bojler či kouřovod?
V článku najdete jednoduchý návod na to, jak si orientačně vypočítat tepelné ztráty, popřípadě tepelné zisky z ploch, jejichž teplota je vyšší než teplota prostředí. Například z pláště kotle, bojleru atp.
Je to ztráta nebo zisk? Otázka, která nás často trápí při kontaktu s teplou trubkou topení, pláštěm bojleru či akumulační nádrže, nebo při pohledu na tetelící se vzduch nad kouřovodem za kotlem. Tak to je otázka, na kterou se v tomto článku nechystám odpovědět. Protože často zbytečné úvahy o ztrátovosti vyřeší jednoduchý výpočet. Nebo naopak zjistíme, že by se s tím mělo konečně něco dělat. Ale nejdříve je nutné zjistit, kolik toho tepla vlastně.
Výpočet sdílení tepla povrchem tělesa má různé úrovně složitosti, podle toho, zda zpracováváte diplomovou práci, chystáte se konečně potvrdit existenci temné hmoty, nebo jen píšete praktickou pomůcku pro majitele domu či bytu. Vzhledem k tomu, že ten první úkol už mám nějakou dobu za sebou, na ten druhý mi chybí ještě doladit pár detailů, pokusím se alespoň poradit, jak si doma můžete jednoduše spočítat, kolik tepla „vyzařuje“ to či ono.
Sdílený tepelný tok
Složité výpočty tepelných toků zahrnují mechanismy přestupu tepla prouděním (konvekcí) a sáláním (radiací). Nám bude stačit zjednodušený výpočet, který vychází ze základního normativního vzorce pro výpočet poměrné ztráty sdílením tepla do okolí u spalovacích zdrojů tepla pro ústřední vytápění (ČSN 07 0240, ČSN EN 304). Podle tohoto postupu se stanoví sdílený tepelný tok Q [W] z plochy o obsahu F [m2] o průměrné povrchové teplotě tm, při teplotě okolí tL podle vztahu
Q = F ∙ α ∙ (tm − tL)
Velikost součinitele přestupu tepla α [W∙m-2∙K-1] je závislá na velikosti povrchové teploty a je rozdílná pro horizontální a vertikální plochy. Ovšem rozdíly jsou pro přibližné výpočty zanedbatelné. Pro jejich získání se využívají různě přesné grafy, já osobně preferuji níže přiložený přehledný graf ze „stařičké“ (ovšem nepřekonatelné) ČSN 07 0240 (Teplovodní a nízkotlaké parní kotle).
Pokud se na jedné velké ploše vyskytují místa se značně rozdílnými teplotami, je nutné tuto plochu rozdělit na dílčí menší plochy s přibližně shodnými teplotami a tepelné toky pro ně spočíst zvlášť. Příkladem může být čelní plocha kotle, na které se nacházejí vedle opláštěním izolovaných míst také neizolovaná přikládací dvířka. Celkový tepelný tok („výkon“) je poté dán součtem dílčích toků z jednotlivých ploch.
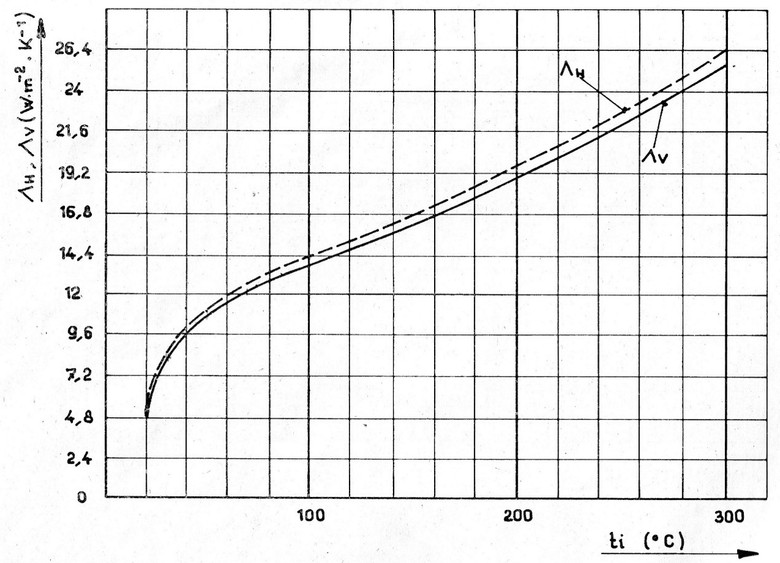
Obr.1 Přibližné hodnoty součinitele přestupu tepla dle ČSN 07 0240, kde ЛH a ЛV představují hodnoty součinitele pro horizontální a vertikální plochu. Jak vidno, rozdíly jsou zanedbatelné.
Kolik vysálá kouřovod?
Tak pojďme rychle k praktickému výpočtu. Aby měl výpočet vůbec nějaký smysl, je nutné se nejdříve přesvědčit o tom, že je teplota „zkoumaného“ povrchu vůbec vyšší jak teplota prostředí. My si tedy vybereme pro modelový výpočet kouřovod, u kterého nehrozí, že bychom počítali tepelný tok zbytečně.
Na zkušebně testuji celou zimu peletový kotel (s retortovým hořákem – pro info některým retorto-pochybovačům). Mezi kotlem a sopouchem komína mám kouřovod o síle stěny 2 mm a o průměru 150 mm, k tomu 2 pravoúhlá kolena. Zajímalo mne, kolik mi „vysálá“ kouřovod do okolí při běžném provozu. Za kotlem jsem na kouřovodu naměřil průměrnou teplotu povrchu 74 °C, v horní části u sopouchu 65 °C. Mimochodem, teplota spalin v ose kouřovodu byla cca 160 °C. Teplota v místnosti byla naměřena 13 °C. Plochu rovného úseku kouřovodu jsem spočítal na 0,48 m2, u kolena pak 0,28 m2, dohromady tedy 1,04 m2. Z grafu jsem odečetl pro střední teplotu povrchu 70 °C „univerzální“ součinitel prostupu α = 12 W∙m-2∙K-1. Celkový tepelný tok je potom
Q = 1,04 ∙ 12 ∙ (70 − 13) = 711 W.
Takový malý radiátor. A hned je mi jasné, proč i za největších mrazů zkušebnu/kotelnu nemusím vytápět, abych měl po celou zimu vnitřní teplotu nad 10 °C. Samozřejmě pomáhá také pár metrů nezatepleného potrubí. Vzhledem k tomu, že teplota spalin i na sopouchu (vstupu do komína) se i tak pohybuje nad 140 °C, není potřeba kouřovod izolovat, protože je to pořád krásná teplota pro suchý provoz komína a celoroční sezónní účinnost zkoušeného kotle vychází na hranici 90 % (měřeno přímou metodou, tedy ze spotřeby paliva a tepla odečteného z kalorimetru).
A co bojler?
Když jsem manželce vysvětlil, co že to měřím a počítám na zkušebně, hned jsem dostal za úkol „zkouknout“ a spočítat i na ten náš nový bojler v koupelně, který se v zadní části nějak přehřívá. Nejjednodušší bylo spočítat plochu válce – 1,5 m2. S teplotou povrchu to bylo horší. Na větší části plochy byla prakticky shodná s teplotou v koupelně, tedy cca 25 °C. Jen vzadu to bylo opravdu teplejší o cca 5 °C, takže jsem si to zjednodušil a dal za celou plochu teplotu 27 °C. Pro teploty blízké pokojové teplotě vychází součinitel přestupu na hranici 5 W∙m-2∙K-1. A kolik tepla nám tedy utíká z našeho bojleru?
Q = 1,5 ∙ 5 ∙ (27 − 25) = 15 W.
Manželka byla spokojená, že se potvrdilo, že „to“ sálá. Ve skutečnosti to bylo trochu jinak. Ta zadní část bojleru byla teplá od nezaizolovaných cirkulačních trubek, kterými je bojler vytápěn, a které jsou vedeny těsně kolem pláště.
V blízké době, příště, se podíváme na ty trubky. Respektive si popíšeme, jak jednoduše vypočíst (či odečíst z vyhlášky) i teplo sdílené neizolovaným potrubím, či jak si orientačně stanovit ztrátu sdílením tepla do okolí u teplovodního kotle (pokud znáte alespoň přibližně jeho výkon a účinnost).
