Model tepelného čerpadla s odvodem tepla na třech úrovních
Snížení teploty otopné vody vracející se do tepelného čerpadla může mít příznivý vliv na jeho energetickou efektivitu. Vyplývá to z experimentu, ve kterém byl z kondenzátoru oddělen samostatný chladič par chladiva a samostatný dochlazovač zkapalněného chladiva.
Úvod
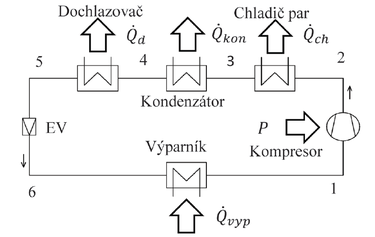
Tepelná čerpadla mají stále velký potenciál rozvoje. Klasické tepelné čerpadlo je velmi jednoduchý stroj, který nevyužívá všechny možnosti odvodu tepla. Na kondenzační straně může být před kondenzátor předřazen chladič par, který odebírá teplo horkým parám po kompresi a umožňuje ohřev teplonosné látky na vysokou teplotu. Tento výměník se již v tepelných čerpadlech některých výrobců používá. Jeho největší předností je možnost při ohřevu otopné vody pro vytápění připravovat zároveň teplou vodu.
Bytové i rodinné domy se stále nižší potřebou tepla k vytápění a starší zateplené domy vykazují celoročně vysoký podíl potřeby tepla na přípravu teplé vody. Běžná tepelná čerpadla v těchto aplikacích mají nízký topný faktor. Použitím dochlazovače jako dalšího výměníku zařazeného do okruhu chladiva pro předehřev studené vody lze zvýšit užitečně odvedené teplo z tepelného čerpadla při současném zachování spotřeby elektrické energie tepelného čerpadla (zvýšit topný faktor).
Pro určení potenciálu tří-výměníkového tepelného čerpadla (kondenzátor + chladič par + dochlazovač) byl vyvinut matematický model tepelného čerpadla, který se následně ověřoval na reálném prototypu.
Matematické modelování tepelných čerpadel a následná aplikace modelu v dalších simulačních prostředích umožňuje s velkou přesností předpovědět chování komplexních systémů, ať již vytápění, přípravy teplé vody nebo jejich kombinací. Problémem je však vytvoření modelu tepelného čerpadla, který by s dostatečnou přesností popsal chování reálného stroje. Existující „statické“ modely tepelného čerpadla vytvoří jeho výkonovou mapu, v níž pak hledají na základě vstupních teplot (průtoky většinou nelze měnit) výstupní teploty, případně výkon a příkon zařízení. Tyto modely však nelze použít pro analýzu změny velikosti výměníků, průtoku, přehřátí chladiva ve výparníku, nebo podchlazení kapalného chladiva v kondenzátoru, protože nejsou schopny reálně predikovat chování zařízení.
Další možnost modelování tepelných čerpadel je založena na základě termodynamického modelu chladiva a jednotlivých komponent (kompresoru, kondenzátoru, výparníku). Každá komponenta může být popsána jednou nebo více rovnicemi, které odrážejí její chování a velikost. Pro kompresor je to například zdvihový objem (respektive výkonnost) a rovnice popisující izoentropickou účinnost a dopravní součinitel. Dalším důležitým vstupem je pracovní obálka kompresoru. Výměníky jsou popsány součinem teplosměnné plochy A a součinitelem prostupu tepla U.
Problematickou součástí modelu je jeho numerický výpočet na základě iteračních přibližování k přesnému výsledku. Numerická matematika v tomto přináší celou řadu inspirativních řešení, ale jejich implementace naráží na komplexnost hledaného řešení a často selhává. Proto byl v případě použitého modelu vytvořen jednoúčelový numerický řešitel konvergující řešení ve všech sledovaných stavech.
Teorie
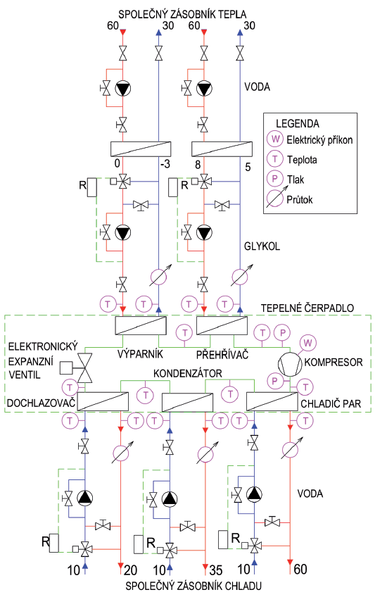
Tepelná čerpadla pracují s levotočivým parním cyklem chladiva. V základním uspořádání se skládají z mnoha komponent, z nichž většina představuje pro modelování reálného stroje pouze tlakovou ztrátu – průhledítko, filtrdehydrátor, potrubí, fitinky atd. Pro modelování jsou nejdůležitějšími komponentami kompresor, jednotlivé výměníky tepla a škrticí ventil. Výparník je napojen na zdroj nízkopotenciálního tepla, kondenzátor, chladič par a dochlazovač na spotřebiče tepla. Celý modelovaný systém je znázorněn na obr. 1 vlevo.
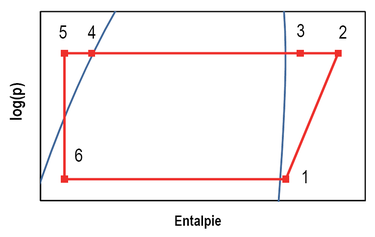
Obr. 1 Schéma zapojení tepelného čerpadla (vlevo) a p-h diagram (vpravo)Tepelný oběh je zobrazen v semilogaritmickém p-h diagramu (obr. 1 vpravo). Jednotlivé procesy sdílení tepla (ve výměnících) jsou znázorněny jako izobary (konstatní tlak), škrcení (na expanzním ventilu) probíhá izoentalpicky (nemění se entalpie) a komprese (v kompresoru) se modeluje jako polytropická (tepelná kapacita se nemění, je konstantní).
Model reálného kompresoru
Model kompresoru vychází z teorie vypracované pro vzduchové kompresory [1]. Kompresor je popsán zdvihovým objemem Vzd, respektive výkonností, dopravním součinitelem λd a izoentropickou účinností ηie. Výkonnost udává objemové množství dodaného plynu při nulovém stlačení (tlakový poměr σ = 1) za časovou jednotku a určí se jako teoretický zdvihový objem kompresoru vynásobený otáčkami n podle rovnice
= Vzd ⋅ n
(1)
kde je
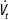
- – výkonnost kompresoru [m3·s−1],
- n
- – otáčky kompresoru [s−1],
- Vzd
- – zdvihový objem kompresoru [m3].
Skutečný hmotnostní průtok dopravovaného plynu je popsán rovnicí
⋅ λd ⋅ ρch,s
(2)
kde je
- ṁch
- – hmotnostní průtok chladiva [kg·s−1],
- λd
- – dopravní součinitel [–],
- ρch,s
- – hustota chladiva na sání kompresoru [kg·m−3].
Dopravní součinitel není při měnících se podmínkách na sání a výtlaku konstantní, ale mění se především se změnou tlakového poměru. Pro dříve často používané pístové kompresory byl nejvíce závislý na velikosti škodlivého prostoru (objem válce, který se nevytlačí během výfuku do výtlaku a z něhož následně stlačený plyn expanduje a zmenšuje tak množství nasátého plynu do pracovního prostoru). Pro dnes používané spirálové kompresory bez škodlivého prostoru je dopravní součinitel při většině provozních stavů velice blízký jedné a lze popsat lineární funkcí podle rovnice [2]
kde je
- C1, C2
- – konstanty [–],
- σ
- – tlakový poměr [–].
Obr. 2 Rozdíl mezi ideální izoentropickou a skutečnou kompresí v p-h diagramu
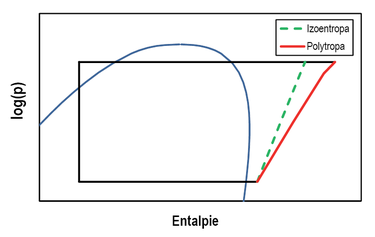
Izoentropická účinnost ηie [–] charakterizuje kompresor energeticky. Reálná komprese je polytropická s proměnným exponentem komprese. Její nejjednodušší popis je pomocí odchylky od izoentropické komprese. Rozdíl mezi skutečnou kompresí a kompresí izoentropickou je na obr. 2.
Izoentropická účinnost je funkcí tlakového poměru a lze ji popsat podle rovnice [2]
kde jsou
- D1 až D5
- – konstanty.
Uvažovaný model kompresoru nejprve na základě podmínek na sání a výtlačného tlaku určí tlakový poměr σ a izoentropickou účinnost ηie, z nich následně hmotnostní průtok chladiva a teplotu na výtlaku, respektive měrnou entalpii chladiva za kompresorem podle rovnice
kde je
- h2
- – měrná entalpie chladiva za kompresorem [kJ·kg−1],
- h1
- – měrná entalpie chladiva na sání kompresoru [kJ·kg−1],
- h2,ie
- – měrná entalpie chladiva po izoentropické kompresi [kJ·kg−1].
Příkon kompresoru P [kW] je určen rovnicí
zt
(6)
kde je
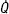- zt
- – ztrátový tepelný tok kompresoru [kW].
Ztrátový tepelný tok kompresoru (vyzáření tepla z povrchu pláště do okolí) výrobci odhadují na 5 % jeho příkonu. U tepelně izolovaných kompresorů je zanedbatelný.
Model výměníku tepla
Za ustáleného stavu musí ve výměníku platit rovnost mezi teplem přivedeným, odvedeným a sdíleným přes teplosměnnou plochu. Uvedený stav je obecně popsán následujícími vztahy:
hx = ṁch ‧ abs(hch,in − hch,out)
pro stranu chladiva (7)
hx = ṁliq ‧ cp,liq ‧ abs(tliq,out − tliq,in)
přivedené/odvedené teplo teplonosnou látkou (8)
hx = UA ‧
δV − δM
ln(δV / δM)
pro prostup tepla (9)
kde je
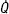- hx
- – tepelný výkon výměníku [kW],
- hch,in
- – entalpie chladiva na vstupu do výměníku [kJ·kg−1],
- hch,out
- – entalpie chladiva na výstupu z výměníku [kJ·kg−1],
- cp,liq
- – měrná tepelná kapacita teplonosné látky [kJ·kg−1·K],
- tliq,in
- – teplota teplonosné látky na vstupu do výměníku [°C],
- tliq,out
- – teplota teplonosné látky na výstupu z výměníku [°C],
- δV
- – větší teplotní spád [K],
- δM
- – menší teplotní spád [K],
- U
- – součinitel prostupu tepla [kW·m−2K−1],
- A
- – teplosměnná plocha [m2].
Dochlazovač je z hlediska fyzikálního popisu nejjednodušší výměník tepla v chladivovém okruhu. Dochází v něm pouze k ochlazování kapalného chladiva. Při správné funkci kondenzátoru v něm nedochází k fázové změně v žádném provozním stavu. Chladič par standardně pracuje také jako výměník, v němž neprobíhá fázová změna, nicméně pokud je teplota vstupující ohřívané teplonosné kapaliny nižší než kondenzační teplota chladiva, část chladiva začíná kondenzovat, což musí model zohlednit. Výparník a kondenzátor jsou výměníky tepla s fázovým přechodem na straně chladiva, proto je nelze modelovat jako jednofázové výměníky, ale pouze jako složené výměníky.
Kondenzátor je složen ze tří částí:
- chlazení par,
- kondenzace,
- podchlazování kapalného chladiva.
Výparník je složen ze dvou částí:
- vypařování,
- přehřívání par.
Model uvažuje kondenzátor jako tři složené výměníky a výparník jako dva. Jejich výstupy jsou logicky provázány. Výrobce výměníků tepla udává součin UA pro konkrétní podmínky. Numerický řešitel se snaží najít pro zadané vnější podmínky (teploty a průtoky na primární a sekundární straně) takovou kombinaci vypařovací a kondenzační teploty, aby zpětně dopočítaná celková hodnota UAcelk výměníku odpovídala UA od výrobce. Celková hodnota UA pro kondenzátor se určí podle rovnice (10) a pro výparník z rovnice (11).
kde je
- (UA)chl
- – součin UA části chlazení par v kondenzátoru [kW·K−1],
- (UA)kon
- – součin UA části kondenzace kondenzátoru [kW·K−1],
- (UA)d
- – součin UA části podchlazování v kondenzátoru [kW·K−1],
- (UA)vyp
- – součin UA části vypařování ve výparníku [kW·K−1],
- (UA)pp
- – součin UA části přehřívání par ve výparníku [kW·K−1].
Okrajové podmínky modelu
Model musí respektovat podmínky nastavené výrobcem tepelného čerpadla. Jsou jimi volba chladiva, přehřátí na výparníku a podchlazení v kondenzátoru. Model umožňuje volbu chladiva implementací knihoven ze softwaru REFPROP [3]. Přehřátí na sání je udržováno expanzním ventilem. U běžných tepelných čerpadel je nastavováno na co nejnižší, ale přitom bezpečnou hodnotu a je konstantní. Velikost podchlazení chladiva za kondenzátorem je dána náplní chladiva v okruhu. Pro větší náplň podchlazení roste, naopak při nedostatečném naplnění může dojít ke vzniku bublin před expanzním ventilem, což snižuje jeho životnost a omezuje funkci.
Zásadní kontrolou správného výpočtu je energetická bilance (vycházející se zákona zachování energie) celého tepelného čerpadla. V ustáleném stavu musí platit rovnost mezi přivedeným a odvedeným tepelným výkonem
vyp = chl + kon + d ± zt
(12)
kde je
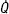- d
- – topný výkon dochlazovače [kW]
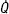- kon
- – topný výkon kondenzátoru [kW]
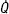- chl
- – topný výkon chladiče par [kW]
- vyp
- – chladicí výkon výparníku [kW]
- zt
- – ztrátový tepelný výkon [kW]
Měření prototypu tepelného čerpadla pro validace
V laboratořích nově postaveného Univerzitního centra energeticky efektivních budov UCEEB ČVUT v Praze bylo postaveno tepelné čerpadlo kapalina-voda z následujících hlavních komponent:
- chladivo R410A
- kompresor Copeland ZH05K1P-TFM [4]
Vt = 4 m3.h−1
λd = 1,047 – 0,0377σ
ηie = −0,7859 + 1,5845σ – 0,603σ2 + 0,0956σ3 − 0,0055σ4 - deskový kondenzátor SWEP B25Tx30 [5]
UA = 1500 W.K−1 - deskový výparník SWEP B25Tx30 [5]
UA = 1215 W.K−1 - deskový chladič par SWEP B8Tx20 [5]
UA = 180 W.K−1 - deskový dochlazovač SWEP B8Tx20 [5]
UA = 270 W.K−1 - přehřátí na výparníku 4 K
- podchlazení kapalného chladiva v kondenzátoru 2 K
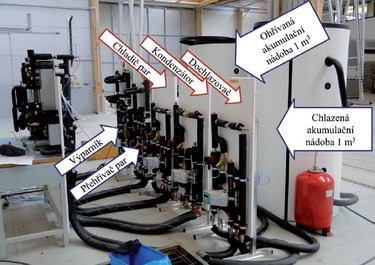
Kvůli testování a variabilitě bylo tepelné čerpadlo doplněno ještě o přehřívač par, kterým lze ohřívat chladivo za výparníkem a zvyšovat jeho teplotu na sání kompresoru. Při měřeních tento výměník nebyl zapojen. Měřený prototyp tepelného čerpadla je zobrazen na obr. 3.
Pro experimentální měření na prototypu byla postavena měřicí trať s pěti měřicími okruhy. Jelikož se jedná o měření tepelného čerpadla s odvodem tepla na třech úrovních, byla vyrobena pro každý výměník samostatná smyčka pro měření jeho výkonu. Na výparník byl napojen měřicí okruh s roztokem glykolu. Nemrznoucí směs byla ohřívána vodou přes oddělený deskový výměník tepla napojený na vytápěnou akumulační nádobu. Všechny výměníky tepla na kondenzační straně chladivového okruhu jsou napojeny přes regulační uzly přímo na chlazenou akumulační nádobu. Měřicí trať v laboratoři UCEEB ČVUT je zobrazena na obr. 4.
Obr. 3 Prototyp měřeného tepelného čerpadla
Obr. 4 Zapojení měřicích smyček
Obr. 5 Schéma zapojení měření tepelného čerpadla
Na jednotlivých měřicích okruzích se pro zjištění výkonu měřil rozdíl teplot a průtok. Na vlastním chladivovém okruhu se měřily teploty a tlaky na nejdůležitějších místech. Příkon kompresoru byl zjišťován wattmetry pro každou fázi kompresoru. Schéma zapojení včetně umístění jednotlivých čidel je uvedeno na obr. 5.
Validace modelu standardního tepelného čerpadla
Obr. 6 Porovnání výkonů, příkonu a topného faktoru tepelného čerpadla z měření a modelu
Standardní tepelné čerpadlo pracuje pouze s kondenzátorem a výparníkem. Tepelné čerpadlo bylo podrobeno zkouškám pro ověření v předchozím textu popsaného modelu. Samotné testování neprobíhalo v souladu s normou ČSN EN 14 511 [6], ale bylo upraveno pro potřeby modelu. Průtoky na kondenzátoru a výparníku byly nastavovány pro každý stav individuálně, tak aby teplotní rozdíl byl přibližně 5 K. Jako nemrznoucí kapalina byla použita směs glykolu a vody s teplotou tuhnutí −15 °C (30 %).
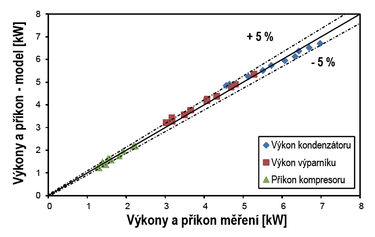
Model dokázal predikovat v jednotlivých měřených bodech výkony s přesností maximálně do ±5 % proti naměřeným hodnotám (obr. 6). Průměrná relativní odchylka výsledků modelu od naměřených hodnot je:
- 2,6 % pro topný výkon kondenzátoru
- 3,3 % pro chladicí výkon výparníku
- 3,7 % pro příkon kompresoru
Obr. 7 Rozložení teplot v okruhu chladiva v t-h diagramu
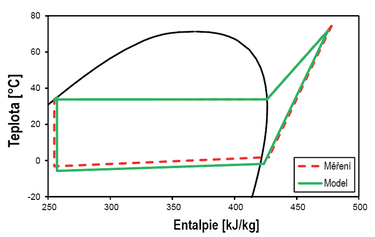
Výsledky modelu tedy velice dobře predikují výkon zařízení. Na tepelném čerpadle byly měřeny teploty a tlaky na chladivovém okruhu. Jejich srovnání je patrné z t-h diagramu oběhu chladiva a teplot na vstupu a výstupu z výměníků. Porovnání pro nominální bod 0/35 °C (0 °C = teplota nemrznoucí směsi na vstupu do výparníku, 35 °C = teplota vody na výstupu z kondenzátoru) je na obr. 7.
Díky tomu, že vlastní model byl sestaven ještě před měřením na základě dat od výrobců jednotlivých komponent a jeho vstupy nebyly modifikovány, je možné jej použít pro odhad výkonů a příkonu obecného tepelného čerpadla (případně i chladicího zařízení).
Validace modelu tepelného čerpadla s dochlazovačem
Obr. 8 Porovnání výkonů a příkonu tepelného čerpadla s dochlazovačem v jednotlivých měřených bodech s modelem
Pro zkoušení více-výměníkových tepelných čerpadel nelze postupovat podle normy [6]. Dochlazovač může sloužit především v aplikacích pro předehřev teplé vody o nízké teplotě a je výhodný, pokud je velký rozdíl mezi teplotou kondenzační a vody na vstupu do dochlazovače. Výsledky a porovnání modelu a měření jsou uvedeny na obr. 8.
Model dosahuje opět poměrně vysoké přesnosti. Relativní odchylka mezi modelem a naměřenými daty je pro výkon kondenzátoru a příkon kondenzátoru do 7 %. Odchylka mezi výkonem dochlazovače z modelu a z naměření je větší pro malé hodnoty, naopak nízká pro vyšší. Pro uživatele je nejzajímavější porovnání topného faktoru tepelného čerpadla s dochlazovačem a bez něj při přípravě teplé vody. Srovnání je na obr. 9. Největší přínos má dochlazovač při vysoké kondenzační teplotě, proto je vhodné jej používat pro předehřev teplé vody při současném ohřevu otopné vody kondenzátorem. Naměřený topný faktor standardního tepelného čerpadla na experimentálním měřicím zařízení při 0/55 °C se zvýší o:
- 19,2 % pro 0/55/20 °C
- 23,6 % pro 0/55/15 °C
- 26,3 % pro 0/55/10 °C
Zápis 0/55/20 °C označuje 0 °C teplotu kapaliny na vstupu do výparníku, 55 °C teplotu vody na výstupu z kondenzátoru a 20 °C na vstupu do dochlazovače.
Validace modelu tepelného čerpadla s chladičem par
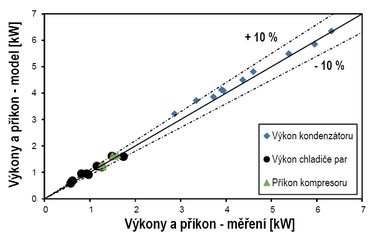
Obr. 9 Porovnání výkonů a příkonu tepelného čerpadla s chladičem par v jednotlivých měřených bodech s modelem
Chladič par umožňuje využít teplo z přehřátých par chladiva za kompresorem. Standardně by teplota vody na vstupu neměla být nižší než teplota kondenzační. Měření tepelného čerpadla s chladičem par proběhlo na zkušebním zařízení. Model vykazuje dobrou shodu s naměřenými hodnotami (viz obr. 9).
Ve většině provozních stavů model přesně popisuje příkon tepelného čerpadla i jednotlivé výkony (s odchylkou maximálně do 10 %), pro topný faktor je shoda do 5 %. Zlepšení shody bude předmětem dalšího vývoje modelu.
Validace modelu tepelného čerpadla s chladičem par a dochlazovačem
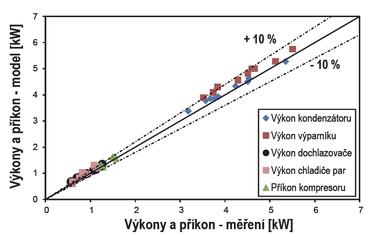
Obr. 10 Porovnání výkonů a příkonu tepelného čerpadla s chladičem par a dochlazovačem zjištěného měřením s modelem
Výpočtový model vykazuje proti měření v tomto nejkomplikovanějším hodnoceném uspořádání nejvyšší relativní odchylky (do 10 % viz obr. 10). Vysokou relativní odchylku má především výkon výparníku, který při správném dimenzování zdroje tepla není pro uživatele rozhodující. Model měl ve většině měřených stavů vyšší topný i chladicí výkon, než bylo změřeno, což je v souladu se zjednodušením modelu (pracuje bez tepelných a tlakových ztrát).
Na obr. 10 je vidět, že v některých bodech je zjištěný chladicí výkon výparníku vyšší, než je topný výkon kondenzátoru. To je způsobeno připojením dochlazovače do okruhu, který zvyšuje chladicí výkon výparníku, a také odvedením části tepla, které by normálně bylo předáno v kondenzátoru, chladičem par.
Možnosti použití modelu
Model lze použít pro optimalizaci konstrukce tepelných čerpadel, při návrhu výměníků tepla, výměně kompresoru a přepočtech na jiné chladivo. Zároveň byl model naprogramován jako samostatná komponenta (type250) v simulačním prostředí TRNSYS [7], v němž lze modelovat celoroční provoz tepelného čerpadla v tepelné soustavě budovy s reálnou spotřebou teplé vody a tepla pro vytápění. Tepelné čerpadlo lze tedy přímo přizpůsobit spotřebě tepla a dále optimalizovat pro dosažení vysokého celoročního topného faktoru SPF [–] při zachování investičních nákladů i ve spojení s akumulační nádobou, oběhovými čerpadly atd.
Možnosti dalšího zlepšení modelu
Omezení je v předpokladu konstantní hodnoty UA výměníků. Teplosměnná plocha je pro různé provozní podmínky konstantní, ale součinitel prostupu tepla se mění v závislosti na mnoha vstupních podmínkách. Za hlavní lze označit průtok chladiva, průtok teplonosné látky a jejich teplotu. U chladiva hraje významnou roli tlak. Parametrizace součinitele prostupu tepla je obtížný problém, kterému se věnuje řada vědeckých prací, přesto doposud neexistuje komplexní teorie parametrizace výměníků tepla s fázovou změnou, kterou by bylo možné aplikovat obecně a bez nutnosti jejich proměření a validace. Přesto nelze očekávat dramatické zvýšení přesnosti.
Závěr
Byl vytvořen obecný model více-výměníkového tepelného čerpadla s kondenzátorem, výparníkem, chladičem par, dochlazovačem, expanzním ventilem a kompresorem, který byl modifikován pro konkrétní výměníky tepla a kompresor, a následně ověřen na reálně postaveném zařízení.
Přesnost modelu standardního tepelného čerpadla v predikci výkonů na straně nemrznoucí směsi i vody je průměrně 3 %. Přesnost určení příkonu kompresoru je průměrně 4 %. Jedná se tedy o velice přesný model. Byly ověřeny rozdíly mezi teplotami na některých místech chladivového okruhu a modelem, která rovněž vykazuje dobrou shodu do 3,5 K.
Model tepelného čerpadla s chladičem par a dochlazovačem má také vysokou shodu s naměřenými daty. Většina měřených bodů vykazuje odchylku do 7 %. Topný faktor pak vykazuje shodu ještě vyšší do 5 %.
Model tepelného čerpadla byl jako modelová komponenta pro použití v simulačním prostředí TRNSYS a bude dále používán pro modelování a optimalizaci výměníků, kompresoru a chladiva v tepelných čerpadlech. Aplikaci modelu lze hledat v simulacích, optimalizaci výměníků, přepočtech na jiná chladiva apod.
Samotné tepelné čerpadlo s odvodem tepla na třech úrovních má potenciální uplatnění především při přípravě teplé vody. Chladič par umožňuje připravit teplou vodu o relativně vysoké teplotě při udržení nižší kondenzační teploty. Výhodou dochlazovače je možnost využít zbytkové citelné teplo chladiva a zvýšit tím teplo užitečně odvedené z tepelného čerpadla při nezvýšeném příkonu tepelného čerpadla. Předcházející výhody lze uplatnit, pokud máme v systému přípravy teplé vody speciální akumulační nádobu nebo sérii akumulačních nádob, které umožní toto výhodné zapojení realizovat.
Článek je věnovaný modelování a experimentálnímu ověření modelu tepelného čerpadla, jehož kondenzátor byl pro možnost analýzy rozdělen na tři samostané výměnky. V první části je popsán model jednotlivých komponent a celkového oběhu chladiva včetně okrajových podmínek. Dále je popsán vyrobený prototyp a měřicí okruhy pro jeho zkoušení včetně umístění jednotlivých čidel. Model tepelného čerpadla byl ověřován experimentálními zkouškami na prototypu. Matematický model dosahuje vysoké shody s měřením pro většinu provozních stavů. Průměrná odchylka naměřených a vypočtených hodnot výkonů je 4 % pro standardní zapojení (pouze výparník a kondenzátor), pro více-výměníkové zapojení je odchylka modelu od měření do 10 %. Ověřený model lze dále použít pro optimalizaci a simulace v dalších výpočetních programech.
Výzkum, který vedl k těmto výsledkům, získal finanční prostředky ze sedmého rámcového programu 7RP/2007-2011 Evropské unie na základě grantové dohody č. 282825 – MacSheep a projektu OP VaVpI č. CZ.1.05/2.1.00/03.0091 – Univerzitní centrum energeticky efektivních budov.
Použité zdroje
- [1] LIŠKA A., NOVÁK P. Kompresory. Vydavetelství ČVUT, 1999.
- [2] DUPREZ M. E., DUMONT E., Frère M. Modelling of reciprocating and scroll compressors. International Journal of Refrigeration. 2007, č. 30, s. 873–886.
- [3] HUBER M., LEMNON E., MCLINDEN M. NIST reference fluid thermodynamic and transport properties – REFPROP [on-line], [aktualizováno 30. 5. 2014]. Dostupné z: http://www.nist.gov/srd/nist23.cfm
- [4] Emerson Climate Technologies. SELECT – Copeland selection software, verze 7.7 [software]. [přístup od 05/13].
- [5] SWEP. SSP G7, verze 7.0.3.24 [software].
- [6] ČSN EN 14511. Klimatizátory vzduchu, jednotky pro chlazení kapalin a tepelná čerpadla s elektricky poháněnými kompresory pro ohřívání a chlazení prostoru. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, 2012.
- [7] KLEIN, S. A., aj. TRNSYS 17: A Transient System Simulation Program. Solar Energy Laboratory, Universita Wisconsin, Madison, USA, 2010.
The paper deals with modelling and experimental validation of the heat pump model with cooler of the vapours and aftercooler. The first part describes model of the individual components and the whole cycle, including boundary conditions. The constructed prototype and measuring circuits are described in the second part, including placement of individual sensors. The model of the heat pump has been verified by experiments on the prototype. The mathematical model shows high correspondence with measurement for most of the operational conditions. The mean deviation of measured and calculated power outputs is 4 % for standard configuration (only evaporator and condenser). For multi-exchanger configuration the model differs from the experiment by 10 %. The validated model can be further used for optimization and simulations in another computational programs.
