Posuzování tepelně izolačních vlastností teplovodního potrubí II.
Část 2 – Teoretické zásady ochlazování vody při průtoku
V článku je odvozen vztah pro ochlazování teplé vody v potrubí v chladnějším venkovním prostředí. Ochlazování a následná tepelná ztráta má tvar exponenciální funkce, která je závislá na exponentu chladnutí.
1. Úvod
Výpočtem se stanovují tepelné ztráty a ochlazování vody průtokem potrubím v závislosti na parametrech:
- tvarových (průřez a délka úseku)
- tepelně technických (teplota vody a okolí, tepelný odpor a součinitel přestupu tepla u stěny)
- hydraulických (objemový průtok a rychlost proudění).
2. Stanovení tepelné ztráty při proudění vody – stacionární stav
Voda proudící potrubím při teplotě TV přenáší při průtoku množství tepla v závislosti na teplotě vody. Obecně množství tepla obsažené ve vodě lze vyjádřit nejčastěji výkonem:
kde je
- ṁ
- průtok vody potrubím [kg/h]
- c
- měrná tepelná kapacita vody 1,163 [Wh/kg.K]
- θi
- aktuální teplota proudící vody v potrubí [°C]
- θo
- teplotní hladina, ke které se vztahuje tepelný obsah vody [°C]
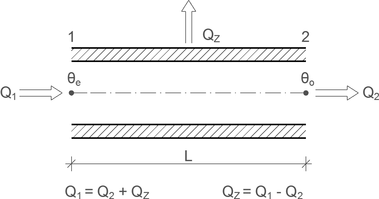
Obr. 1 Schéma změny výkonu ochlazováním při průtoku vody potrubím v úseku 1 až 2
Q1 – vstupní výkon při teplotě θe, Q2 – výstupní výkon při teplotě θo, QZ – tepelná ztráta stěnou potrubí v úseku délky L
Při proudění teplé vody potrubím z počátečního bodu 1 do koncového bodu 2, podle obr. 1, se voda z počátečního výkonu Q1 ochladí na výkon Q2 ve výstupním bodě 2. Na délce potrubí (L) je toto ochlazení vody vyjádřeno výkonem (tepelnou ztrátou) (QZ). Zobrazení tohoto výpočtového předpokladu je na obr. 1.
Prostupem tepla stěnou potrubí dochází ke snižování teploty vody ve směru jejího průtoku. V předchozím odstavci byly stanoveny vztahy pro výpočet prostupu tepla při setrvalém stavu. Uvažujme zatím rovněž ochlazování vody okolním prostředím při ustáleném – setrvalém stavu, tj. kdy veškerá ztráta tepla ochlazováním vody projde stěnou potrubí, aniž bychom potřebovali teplo na ohřátí stěny potrubí a izolace.
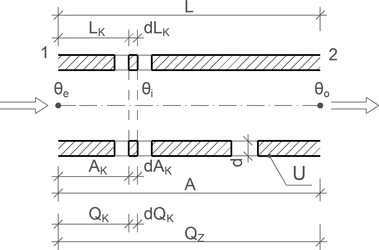
Obr. 2 Výpočtové schéma ochlazování vody protékající potrubím a stanovení tepelné ztráty
θ – teplota, U – součinitel prostupu tepla, d – tloušťka stěny, A – plocha povrchu stěny (vrstvy), QZ – množství tepla – výkon (tepelná ztráta)
Indexy: řada 1, 2, 3 ... pořadí úseků; u – vnější (okolí), e – vstupní, o – výstupní
Schematicky představu tvaru a parametrů potrubního úseku máme zobrazenou na obr. 2. Uvažujme potrubí délky (L) se vstupní teplotou vody (θe), výstupní teplotou vody z potrubí (θo), proměnnou teplotou vody (θi), se stěnou potrubí tloušťky (d) a součinitelem prostupu tepla (U).
Ve vzdálenosti (LK) od místa vstupu vody do potrubí je teplota vody (θi) v diferenciálu délky (dLK). Po délce (LK) prochází teplo od vody QK plochou potrubí AK tak, že přírůstek ochlazování vody dQK je na diferenciálu plochy (dAK). Celková ochlazovaná plocha potrubí je (A) a celkové ochlazení vody na délce potrubí (L) od bodu 1 do bodu 2 je QZ.
Potrubím proudí voda hmotnostním průtokem ṁ (kg/s) a s konstantní měrnou tepelnou kapacitou cv.
Na diferenciálu plochy potrubí dAK je tepelná ztráta prostupem tepla vyjádřena vztahem:
Množství tepla, které projde plochou AK, se stanoví ze vztahu:
3. Stanovení exponentu chladnutí
Úpravou předchozích vztahů bude proměnná teplota vody v potrubí vyjádřena:
Po dosazení vztahu (2) do rovnice (1) získáme:
Úpravou vztahu (3) dostaneme rovnost:
Provedeme-li integraci v mezích 1–2 (od 0 do Q; od 0 do A) dostaneme po úpravě rovnici:
Pravá část rovnice, bezrozměrné číslo, se nazývá často exponent chladnutí a je označován symbolem (K). Pro něj platí vztah:
kde je
- O
- vnitřní obvod potrubí [m]
- L
- délka potrubního úseku [m]
4. Stanovení výstupní a střední teploty vody v úseku potrubí
Z rovnice (5) získáme exponenciální vztah průběhu teplot:
Odtud osamostatněním Q (množství tepla, které projde stěnou potrubí) získáme vztah:
Z rovnice (5) pak můžeme stanovit, jaká je výstupní teplota vody z potrubí:
Z toho plyne vztah pro výpočet tepelné ztráty při průtoku:
Úpravou získáme nejčastěji používaný vztah pro výstupní teplotu vody:
Střední teplota vody (θm) se pak vyjádří ze vstupní teploty (θe) a teploty okolí potrubí (θu) ze vztahu:
5. Význam a použití exponentu chladnutí
a) Průběh ochlazování vody v potrubí a stanovení tepelné ztráty v rozvodech
Z výše uvedených vztahů plyne, že ochlazování vody při průtoku potrubím a následně tepelná ztráta v rozvodech má průběh exponenciální.
Lineární průběh ochlazování, který je často uváděn i ve výpočtových návodech, vychází z topenářské zkušenosti, kdy se potrubí považuje za otopnou plochu vytvořenou ze segmentů předávajících teplo v závislosti na dodaném množství tepla (průtoku vody).
Průběh změny teploty vody (změny tepelné ztráty) je dále posuzován na exponentu chladnutí K (vztah 6), ve kterém jsou proměnné hodnoty:
- součinitele prostupu tepla U,
- vnitřní plocha potrubí O ‧ L,
- průtok vody ṁ.
b) Změna součinitele prostupu tepla podle proměnné rychlosti proudění vody
Součinitel prostupu tepla je závislý na tepelné vodivosti a součiniteli přestupu tepla na straně vodní hi a součiniteli přestupu tepla na straně vzduchové he.
Při změně průtoku vody v potrubí v mezích rychlosti od 0,2 do 2 m/s je změna součinitele přestupu tepla na vnitřním povrchu zanedbatelná, vzhledem k celkové hodnotě součinitele prostupu tepla. Součinitel přestupu tepla na vzduchové straně je závislý zejména od proudění vzduchu okolo potrubí. V uvažovaném místě vedení potrubí je jeho hodnota konstantní.
Pro další posuzování proměnnosti teploty v závislosti na jejím průtoku uvažujeme tedy konstantní hodnotu součinitele prostupu tepla (U).
Součinitel prostupu tepla zahrnuje většinou v seriozních podkladech v sobě jak prostup tepla, tak i předání tepla sáláním. Dále se s touto skutečností při dalších výpočtech uvažuje.
c) Tepelný odpor stěny potrubí
V exponentu chladnutí (K) je tepelný odpor stěny potrubí vyjádřen pomocí součinitele prostupu tepla (U). Z předchozího plyne, že jeho změna proměnnou rychlostí je zanedbatelná.
Tím, že součinitel prostupu tepla je v čitateli součinitele chladnutí a je v poměru k vysoké hodnotě konstantní měrné tepelné kapacity vody, je jeho podíl na ochlazování vody významný.
Z průběhu exponenciálního součinitele eK, který v závislosti na rychlosti má průběh zpočátku strmý a dále pozvolnější, se pak stanovuje optimální tloušťka tepelné izolace. Zvýšená tepelná izolace potrubí je podstatnou složkou úspor tepla – zárukou nízké tepelné ztráty.
d) Ochlazovaná plocha potrubí
V čitateli exponentu chladnutí (K) má rovnocenný podíl na velikosti tepelné ztráty i ochlazovaná plocha potrubí, vyjádřená součinem O ‧ L (kde O je vnitřní obvod potrubí a L je délka potrubí). Při návrhu je průřez potrubí funkcí rychlosti.
U potrubí přívodu TV je rychlost v proměnných mezích od minimálního průtoku v případě, že není odběr vody, do maximálního průtoku při špičkovém odběru TV. U cirkulačního potrubí se průtok mění méně.
Obecně by měla platit zásada nepředimenzovat zbytečně potrubí, zejména u cirkulačního vedení, a raději volit oběhová čerpadla s vyšším dispozičním tlakem. Dosavadní praxe je většinou opačná, a protože při projektování nejsou dostatečné podklady o průběhu odběrů, cirkulační potrubí nebývá většinou hydraulicky posuzováno. V důsledku toho jsou veškeré sítě předimenzované s tím, že se argumentuje úsporami na výkonu oběhových čerpadel. Zapomíná se, že předimenzování průměru potrubí trubní sítě vede k významným tepelným ztrátám z větší prostupové plochy, a to zejména u potrubí nedostatečně izolovaného.
6. Dělení trubní sítě na úseky
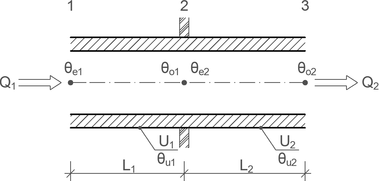
Obr. 3 Výpočtové schéma pro dva navazující úseky potrubí se změnou teploty okolí θu, resp. s jinými parametry tepelné izolace
θe – vstupní teplota vody do úseku i, θo – výstupní teplota vody z úseku i, U – součinitel prostupu tepla stěny potrubí a vrstvy tepelné izolace
Indexy i-tého úseku: 1 – platí pro úsek 1 až 2, 2 – platí pro úsek 2 až 3
Podle změny parametrů trubní sítě je výpočtové schéma, uvedené na obr. 2, platné vždy v daném úseku s konstantními parametry. Při běžném větveném trubním rozvodu jsou jednotlivé úseky pro výpočtové podmínky dány mezi odbočkami pro přítok, resp. odtok vody. Úseky jsou charakteristické odlišností různých konstantních rychlostí, resp. průtoky vody potrubím.
Změna parametrů trubní sítě může být však dána také změnou teploty okolí (např. při přechodu z vnitřního prostoru do zemního vedení). Rovněž za změnu parametrů je považován i různý tepelný odpor tepelné izolace, který je vyjádřen nejčastěji součinitelem prostupu tepla (U).
Na obr. 3 je naznačeno výpočtové schéma změny parametrů součinitele prostupu tepla (U) a teploty okolí (θu) v úseku délky (L1) mezi body 1 až 2 a v úseku délky (L2) mezi body 2 až 3.
Pro výpočet v daných úsecích jsou teploty vody v mezních bodech vyjádřeny rovností vstupní a výstupní teploty:
Při výpočtu tepelných ztrát trubní sítě se postupuje po jednotlivých úsecích ve směru průtoku vody.
Posuzování tepelně izolačních vlastností teplovodního potrubí.
- Část 1 – Prostup tepla stěnou potrubí
- Část 2 – Teoretické zásady ochlazování vody při průtoku
- Část 3 – Příklad výpočtu exponenciálního průběhu ochlazování
- Část 4 – Navrhování tepelné izolace podle ČSN EN 12 828
- Část 5 – Příklady ochlazování potrubí u teplovodního vytápění
Předložený soubor článků řeší aplikaci teorie sdílení tepla na problematiku ochlazovaní teplovodního potrubí.
V první části je shrnuta obecná teorie prostupu tepla stěnou potrubí aplikovaná na rovinnou stěnu a potrubí kruhového průřezu. Závěr první části je zaměřen na stanovení součinitele prostupu tepla potrubí.
Druhá část článku řeší problematiku ochlazování potrubí v tepelné síti a aplikace teoretických postupů na ochlazování cirkulačního potrubí teplé vody.
Třetí část na příkladu exponenciálního průběhu ochlazování za různých extrémních okrajových podmínek demonstruje účinek tepelné izolace potrubí a v závěrech jsou shrnuty hlavní faktory ovlivňující ochlazování potrubí s teplonosnou látkou.
Ve čtvrté části pak autor řeší otázky spojené s normovým návrhem tepelné izolace potrubí tepelných soustav v budovách a v přehledných tabulkách uvádí základní parametry a hodnoty potřebné pro výpočet.
V závěrečné, páté části článku jsou aplikovány teoretické principy na teplovodní otopnou soustavu a je zdůrazněn vazba mezi tepelnou ztrátou potrubní sítě a rychlostí proudění teplonosné látky.
Soubor článků představuje ucelený pohled na teorii i praxi problematiky izolace potrubí s podrobným teoretickým základem i příklady aplikace. Doporučuji k publikaci.In article is derived relation for cooling of warm watter in tube in cooler outside ambient. Cooling and consequential heat loss has form of exponential function which is dependent on exponent of cooling.