Stanovení neurčitosti vstupních údajů potřeby tepla na vytápění speciálními metodami
Metódu Monte Carlo môžme aplikovať na citlivostnú analýzu ako aj na analýzu neurčitosti. Metóda Monte Carlo je založená na náhodnom výbere vygenerovaných náhodných veličín všetkých vstupných parametrov X.
1 Úvod
Pre výpočet potreby energie sa v budovách používajú stacionárne mesačné zjednodušené metódy uvedené v STN ISO 13790: 2008 [7]. Presnosť tohto hodnotenia závisí od úrovne podrobnosti výpočtového modelu a od spoľahlivosti vstupných údajov. Súbor týchto vstupných údajov rozdeľujeme vo výpočtových metódach do troch skupín: klimatické údaje, údaje o vonkajších konštrukciách a údaje o užívaní budovy. Vyjadrenie neurčitosti týchto údajov funkciami rozdelenia pravdepodobnosti a aplikácia stochastických metód typu Monte Carlo umožňujú tvorbu intervalu spoľahlivosti a triedy neurčitosti posúdenia energetickej náročnosti budovy. Citlivostnú analýzu a analýzu neistoty je vhodné využiť vo fáze projektu alebo vo fáze návrhu systému. V značnej časti sa snažíme reálny stav popísať matematickým modelom z dôvodu analýzy a optimalizácie. Matematický výpočtový model väčšinou považujeme za veľmi presný, ale vo v skutočnosti však napr.: reálny systém nemôže byť úplne identifikovaný vzhľadom k nepresnosti merania, teoretické zámery projektanta nemôžu byť splnené presne vzhľadom k výrobným toleranciám, matematické modely sa často zámerne idealizujú či zjednodušujú vzhľadom na potrebu jednoduchosti riešenia. Mnohé úlohy však nemožno riešiť bez zjednodušenia modelu, použitím rôznych simulačných softvérov počítajúci s inými výpočtovými algoritmy sa dopúšťame aj nepresnosti [4].
2 Stochastický model
Stochastický model je model, ktorý opisuje systém tak, že berie do úvahy náhodné, ako aj plánované udalosti. Základné výpočtové jadro modelovaného fyzikálneho procesu v energetických výpočtoch predpokladáme v tvare:
kde je
- F
- – výpočtový deterministický model
- Xi
- – náhodné vstupné veličiny parametra
V prípade, keď výpočtový model popisuje daný fyzikálny jav, poskytuje veličina Y výsledok získaný stochastickou analýzou vstupov získaných experimentálnym meraním.
Parametre musia byť definované pomocou pravdepodobnostných vzťahov. Pri opise stochastických modelov sú preto využívané parametre pravdepodobnosti ako sú náhodné premenné, hustota rozdelenia a funkcie rozdelenia.
2.1. Pravdepodobnosť
Pravdepodobnosť je hodnota vyčísľujúca istotu respektíve neistotu výskytu určitej udalosti. Skúma ju teória pravdepodobnosti. Pravdepodobnú hodnotu nadobúdajú náhodné premenné.
Teória pravdepodobnosti alebo počet pravdepodobnosti je odvetvie matematiky, ktoré umožňuje nachádzať podľa pravdepodobností jedných náhodných udalostí iné náhodné udalosti, ktoré nejakým spôsobom súvisia s prvými. Je vhodná na opísanie experimentov, ktoré aj pri nezmenených podmienkach môžu viesť k rozličným výsledkom.
2.2. Rozdelenie pravdepodobnosti v oblasti modelovania spoľahlivosti
V dnešných teoretických poznatkoch existuje veľa normovaných štatistických rozdelení, ktoré môžu byť používané pre modelovanie rôznych parametrov spoľahlivosti. Je zistené, že len pomerne malý počet štatistických rozdelení vyhovuje väčšine potrieb v oblasti spoľahlivosti. Použitie jednotlivých rozdelení závisí v každom prípade od určitosti údajov.
Rozdelenie pravdepodobnosti možno tiež chápať ako zobrazenie, ktoré každému elementárnemu javu priraďuje určité reálne číslo, a ktoré charakterizuje pravdepodobnosť tohto javu. Najčastejšie používané rozdelenia pravdepodobnosti sú:
- Diskrétne rozdelenia pravdepodobnosti:
- Alternatívne rozdelenie (X nadobúda iba dvoch hodnôt 0 alebo 1)
- Rovnomerné rozdelenie (napríklad hod kockou)
- a iné
- Spojité rozdelenie pravdepodobnosti:
- Rovnomerné rozdelenie
- Normálne rozdelenie (označované aj ako Gaussove rozdelenie)
- Logaritmicky normálne rozdelenie (tiež log-normálne rozdelenie)
- a iné
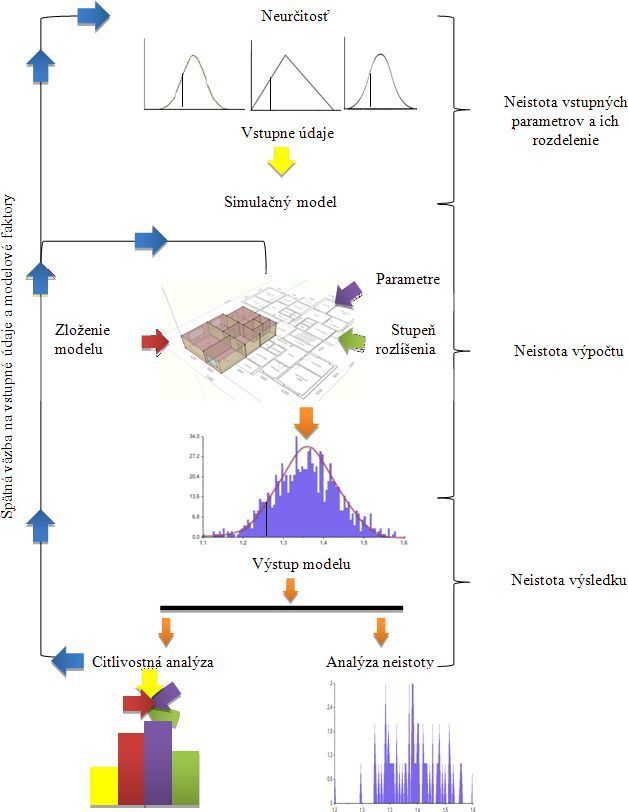
Obr. 2.1 Vývojový diagram výpočtu potreby tepla na vykurovanie pomocou stochastického modelu
3 Citlivostná analýza a analýza neistoty
Analýza citlivosti (CA) sa zaoberá tým, ako môže neistota vstupných parametrov vplývať na výsledné hodnoty výpočtovej analýzy, pričom ďalej skúma vplyv všetkých zdrojov neistoty vo vstupoch modelu.
Analýza neistoty (AN) určuje neistotu premenných, používa sa pri vyhodnocovaní výsledkov, kladie za cieľ vytvárať technický prínos k rozhodovaniu, pomocou kvantifikácie neistoty určitých premenných.
Súbor vstupných údajov potrebných vo výpočtových metódach pre energetické hodnotenie budov možno rozdeliť do troch skupín: klimatické údaje, údaje o vonkajších konštrukciách a údaje o užívaní budovy.
Údaje o užívaní budovy, ktoré ďalej boli bližšie špecifikované a skúmané v iných publikovaných člankoch: vnútorná teplota, intenzita výmeny vzduchu a vnútorné tepelné zisky.
Vyjadrenie neurčitosti týchto údajov funkciami rozdelenia pravdepodobnosti a aplikácia stochastických metód typu Monte Carlo umožňujú tvorbu intervalu spoľahlivosti a triedy neurčitosti posúdenia energetickej náročnosti budovy. Citlivostná analýza jednotlivých zložiek tepelnej bilancie budovy umožňuje určiť najdôležitejšie parametre výpočtového modelu a brať do úvahy neurčitosti vo výstupe modelu [2].
V oblasti techniky sú využívané rôzne metódy, najznámejšie sú Monte Carlo a Morrisova metóda, ktoré boli aplikované na ďalší vývoj práce.
3.1 Metódy citlivostnej analýzy a analýzy neistoty
Je veľké množstvo metód analýzy citlivosti a neistoty. Použitie každého typu záleží na našom zámere, čo presne chceme skúmať a ako to chceme skúmať. Zvolenú metódu Monte Carlo môžeme aplikovať ako na CA, tak aj na a AN.
Monte Carlo je založená na náhodnom výbere vygenerovaných náhodných veličín všetkých vstupných parametrov X. Náhodné hodnoty všetkých vstupov X sa použijú v deterministickom výpočtovom modeli, kde dostaneme výsledok ako hodnotu náhodného javu. V každom kroku simulácie je vybraný práve jeden súbor náhodných veličín všetkých vstupných parametrov [5].
Zvolená Morrisova metóda je založená na variácii vstupných premenných a používa sa pre CA. Funguje na nasledujúcom princípe: v každom výpočtovom kroku je vybraná len jedna náhodná veličina výberu a ostatné vstupné parametre zostávajú konštantné, potom sa vykoná výpočet, vyhodnotí sa zmena výstupov Y a pokračuje ďalej až po posledný parameter [1].
4 Metóda Monte Carlo
Metóda Monte Carlo (MC) predstavuje širokú triedu výpočtových algoritmov využívaných pri stochastickom modelovaní. Metóda je nazvaná podľa Monte Carla, známeho svojimi kasínami a najmä ruletou. Termín prvýkrát použili fyzici v roku 1940 pracujúci na zostrojení americkej atómovej bomby. Rozlišujú sa dva varianty metódy Monte Carlo: analógový a neanalógový model.
Pri analógovom modeli musíme vedieť modelovať celú situáciu na počítači, to znamená poznať všetky rozdelenia pravdepodobnosti skúmaných javov a fyzikálne zákonitosti, ktorými sa riadia. Aplikáciou tejto simulácie získame výsledok, realizáciu akejsi náhodnej veličiny ξ. Túto simuláciu aplikujeme n-krát a získame súbor histórií x1 ...xn.
Neanalógový model je taký prípad, keď pri výpočte nepoužívame model reálneho deja (napríklad výpočet určitého integrálu, prípadne obsahu ohraničeného útvaru). Typicky je využívaná pre výpočet integrálov, najmä viacrozmerných, kde bežné metódy nie sú efektívne.
Metóda Monte Carlo má široké využitie od simulácie experimentov, cez počítanie určitých integrálov, až po riešenie diferenciálnych rovníc. Základná myšlienka metódy je veľmi jednoduchá: chceme určiť strednú hodnotu veličiny, ktorá je výsledkom náhodného deja. Vytvorí sa počítačový model tohto deja a po prebehnutí dostatočného množstva simulácií sa môžu dáta spracovať klasickými štatistickými metódami, napríklad určiť priemer a smerodajnú odchýlku. Výhodou stochastických metód je to, že sú univerzálnejšie ako deterministické, avšak výpočet trvá dlhšie.
MC-Latin Hypercube Sampling (LHS) je forma stratifikovaného náhodného vzorkovania, ktoré môže byť použité pre viac premenných. Metóda sa bežne používa na zníženie počtu simulácií oproti metóde Monte Carlo, s cieľom dosiahnuť primerane presnú distribúciu náhodnej premennej. LHS môže byť začlenené do existujúceho Monte Carlo modelu pomerne ľahko a používa premenné s ľubovoľným analytickým rozdelením pravdepodobnosti. Monte-Carlo simulácie poskytujú štatistické odpovede na problémy prevedením mnohých výpočtov s náhodnými premennými a analýzu trendov výstupných dát.
Analýza Monte Carlo je založená na opakovanej simulácii; žiadané výstupy sú hodnotené pre každý vzorkový prvok xij z matice vzorky Mnk , kde n je číslo vstupného faktora a k je veľkosť vzorky. Výstupný vektor Y = [yi] je potom generovaný ako:
Latin Hypercube Sampling dosahuje lepšie pokrytie priestoru vzoriek vstupných faktorov. Priestor vzorky S vstupného faktora Xi je rozdelený do h disjunktné1 intervaly S ... Sh s rovnakou pravdepodobnosťou 1/h. Z každého intervalu Si je potom vybraná jedna náhodná vstupná hodnota a tento proces sa opakuje k krát, kde k je dĺžka vzorky.
5 Morrisova metóda
Cieľom Morrisovej metódy je určiť, ktoré vstupné faktory môžu byť považované za účinné, ktoré sú zanedbateľné, lineárne a aditívne, alebo nelineárne alebo majú interaktívne účinky. Metóda je založená na analýze rozdelení elementárnych účinkov každého vstupného parametra Xi.
- nastavenie p-úrovne siete: Mriežka vstupu p-úrovne Xi zodpovedá súboru hodnôt vstupných údajov pri p-kvantiloch. Xij môže mať jednu hodnotu z {a1, a2, ..., ai, ...ap} ako
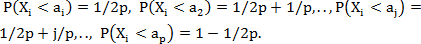
Napríklad, ak Xi je rozdelené normálne s μ = 7 a σ = 2 a pre 4úrovňovú sieť je súbor vstupov {4,71; 6,36; 7,63; 9,29}. - ukážka generovania: Najprv je vstup n vstupový vektor označený ako hodnota náhodnej základne (z diskretizovanej siete definovanej v predchádzajúcom). Cesta krokov diskretizovanou sieťou je realizovaná po jednotlivých krokoch, zatiaľ čo hodnoty iných faktorov sú držané na svojich posledných hodnotách
- konečné rozdelenie Fi : Elementárny účinok Δi x sa vypočíta ako:
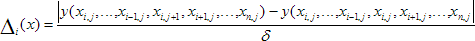 (5.1)
(5.1)
kde δ je násobok z 1/p. Takto n sa získajú konečné rozdelenia Fi s elementárnych efektov pre rôzne vstupné faktory. Rozdelenie Fi je charakterizované svojim priemerom a smerodajnou odchýlku (μM, σM). Vysoký priemer indikuje faktor s významným celkovým vplyvom na výstup, vysoká štandardná odchýlka indikuje, či je faktor interaktívny s inými faktormi, alebo faktor, ktorého účinok je nelineárny [6].
Postup vyvinutej analýzy je zobrazený na obrázku 5.1. Zahŕňa definíciu vstupných údajov a neistôt, náhodné vzorkovanie (pomocou simulačného softvéru Monte Carlo Simlab 2.2, tepelné modelovanie [7] a spracovanie analýzy (Simlab 2.2).
![Obr. 5.1 Postup pri simulácii neurčitosti a citlivosti [3]](/docu/clanky/0122/012255o4.png)
Obr. 5.1 Postup pri simulácii neurčitosti a citlivosti [3]
6 Záver
V súčasnosti je aktuálna potreba zohľadňovať tieto neurčitosti aplikáciou stochastických metód pri modelovaní prenosu tepla a hmoty, zavedením analýzy spoľahlivosti a upresnenie vstupných údajov najviac vplývajúcich na neurčitosť výpočtu potreby tepla na vykurovanie. Zaujímavosťou je porovnanie výsledkov simulácií potreby tepla na vykurovanie pomocou prevádzkového hodnotenia a výpočet podľa normalizovaného hodnotenia s rovnakým testovacím rokom. Ďalej vykonať citlivostnú analýzu a analýzu neurčitosti celkového výpočtu a zamerať sa na neurčitosti (vnútorná teplota, intenzita výmeny vzduchu a vnútorné tepelné zisky).
Ďalej musíme podotknúť na parametre, ktoré sú závislé na ľudskom správaní, ako je vetranie, vnútorná teplota a vnútorné zdroje tepla. Obyvatelia ovplyvňujú niektoré z týchto faktorov v snahe získať príjemné podmienky, napr. otvárajú okná s cieľom znižovať vnútornú teplotu a preto sa zvyšuje intenzitu vetrania. Správanie užívateľov je náhodné a je reprezentované trojicou vstupných údajov vyplývajúcich z ich požiadaviek na tepelnú pohodu: vnútorná teplota, intenzita výmeny vzduchu a z ich počtu v byte.
Literatúra
- [1] Campolongo, F. et al., (1997) Sensitivity analysis of an environmental model: an application of different analysis methods. Reliability Engineering and System Safety, 57.
- [2] Corrado, V. et al., ( 2007) Assessment of building cooling energy need through a quasi-steady state model: Simplified correlation for gain-loss mismatch. Energy and Buildings, 39.
- [3] Corrado, V. and Mechri H. E, (2009) Uncertainty and Sensitivity Analysis for Building Energy Rating. Journal of Building Physics, 125–156.
- [4] Jokisalo, J. et al., Performance of EN ISO 13790 utilisation factor heat demand calculation method in a cold climate. Energy and Buildings, 39.
- [5] KOTEK, P. (2007) Metoda MonteCarlo jako optimalizace energetické náročnosti budov, Praha, ČR.
- [6] Saltelli, A. et al. (2004) Sensitivity analysis in practice: A Guide to assessing scientific models.
- [7] STN EN ISO 13790:2004 Tepelnotechnické vlastnosti budov.Výpočet potreby energie na vykurovanie.
Poznámky
1 disjunktný – nemajúci spoločný prvok... Zpět
We can apply Monte Carlo method to the sensitivity analysis and the analysis of uncertainty, too. The method Monte Carlo is based on random choice of variables generated for all input parameters X.