Modelování operativní teploty
V souvislosti s rozvojem potenciálu výpočetní techniky se objevují nové možnosti využití nového přístupu k řešení inženýrských problémů. Netradiční řešení budov a jejich energetického chování, která bylo dříve nutno otestovat výhradně na skutečných modelech, je v současnosti možné zpracovat již v koncepční fázi do matematického modelu počítačovou simulací proměnlivých okrajových podmínek, sledovat, vyhodnocovat chování modelovaného systému, hledat kritická místa a optimální řešení. Nová technologie zkoumání chování budov simulací na matematickém modelu s sebou přináší i mnohá úskalí. Tak jako u fyzického modelu v měřítku se zanedbávají určité detaily, tak i u modelu matematického je jeden ze základních předpokladů úspěchu správná míra zjednodušení celého problému a nastavení okrajových podmínek. Na rozdíl od fyzického modelu je matematický model daleko citlivější na chybu a není výjimkou, že výsledky při prvních aproximacích matematického modelu se liší od předpokládané skutečnosti. Nutným krokem při matematickém modelování je proto validace modelu, kdy se matematický model ověří na známých skutečně naměřených hodnotách a použitím výsledných parametrů se "naladí" tak, aby výsledky odpovídaly skutečnosti.
Matematické modely, které se postupně začínají používat nejen na úrovni výzkumných úloh, ale i na úrovni inženýrské praxe, se v zásadě dělí na modely statické a dynamické. Modely statické popisují řešený problém v ustáleném stavu a nezohledňují časovou závislost změny parametrů a jsou určeny především pro analýzu prostorových problémů řešících například rozložení povrchových teplot na konstrukcích. Modely dynamické jsou určeny k analýze časově závislých přechodových jevů a popisují tedy i dynamické vlastnosti modelovaných systémů.
Snahy o vytvoření matematického modelu výsledného stavu vnitřního prostředí jsou známy od prvopočátku rozvoje vědních disciplín, které se touto problematikou zabývají. Problém, který až doposud znemožňoval detailní analýzu výsledného stavu vnitřního prostředí byl dán omezenou kapacitou počítačů, které pro modelování tak složitých jevů musí vykonat stovky tisíc matematických operací v relativně krátké době.
1. TEPELNÁ POHODA A OPERATIVNÍ TEPLOTA
Optimální tepelné pohody je dosaženo při rovnováze tepelné bilance člověka [14], kdy produkce metabolického tepla, daného fyzickou aktivitou, je v rovnováze s teplem odváděným z lidského těla do okolního prostředí při dodržení požadovaných rozmezí asymetrie sálavé a konvekční složky sdílení tepla a prostorové asymetrie operativní teploty [12].
Pro hodnocení tepelného stavu prostředí v obecném bodu prostoru podle rovnice tepelné pohody je nutno znát zvlášť teplotu vzduchu ta a povrchovou teplotu jednotlivých okolních ploch tp. Povrchové teploty jednotlivých ploch, kterých je ve skutečnosti nekonečný počet, se v praxi nahrazují jedinou hodnotou, kterou je střední radiační teplota okolních ploch tr. Střední radiační teplota okolních ploch je povrchová teplota imaginárního šedého povrchu obklopujícího daný bod, která má stejné sálavé účinky jako skutečné okolí posuzovaného bodu.
Na rozdíl od jednotlivých povrchových teplot zohledňuje střední radiační teplota vzdálenost posuzovaného bodu od jednotlivých povrchů a jejich poměrnou velikosti (tzv. view factor - poměr osálání) a je tedy již vázána na daný bod v prostoru. U interiérů s rovnoměrnou povrchovou teplotou okolních ploch je vliv posuzovaného místa v prostoru malý, u interiérů s velkými chladnými resp. horkými povrchy je tento vliv podstatný a nezanedbatelný - střední radiační teplota bude zcela jiná v těsné blízkosti a ve velké vzdálenosti od chladné stěny.
Kritérií pro posuzování tepelné pohody je obecně celá řada. Pro zjednodušení hodnocení tepelné pohody se zavádí veličina nazávaná operativní teplota to [°C], která jedinou hodnotou zahrnuje vliv konvekční výměny tepla a vliv sdílení tepla sáláním.
Z hlediska fyzikálního je operativní teplota veličina, která vyjadřuje sálavou a konvekční složku sdílení tepla mezi člověkem a okolním prostředím.
Operativní teplota je vypočtená hodnota a je definována jako jednotná teplota uzavřeného prostoru (tj. prostoru o stejné teplotě vzduchu i stejné střední radiační teplotě), černého z hlediska radiace, ve kterém by lidské tělo sdílelo konvekcí i sáláním stejné množství tepla jako ve skutečném, teplotně nesourodém prostředí [1].
Rovnice (1.1) popisuje sdílení citelného tepla mezi povrchem lidského těla (oblečení a pokožka) a mezi povrchy okolních ploch v interiéru (včetně zdrojů tepla) a mezi okolním vzduchem v interiéru.
| R + C = fcl [hr (tcl - tr) + hc (tcl - ta)] | (1.1) | ||
| AD = 0,202 m0,425h0,725 | (1.2) | ||
| fcl = |  |
1,00 + 0,2 Icl pro Icl ≤ 0,5 clo 1,05 + 0,1 Icl pro Icl > 0,5 clo |
(1.3) (1.4) |
| R | tepelný tok sáláním (radiací) [W.m-2], |
| C | tepelný tok prouděním (konvekcí) [W.m-2], |
| fcl | poměr povrchu těla pokrytého oděvem Acl a povrchu neoblečeného těla AD [-]; podle Fangera - viz rovnice (1.4), |
| hr | součinitel přestupu tepla sáláním (radiací) [W.m-2.K-1]; viz rovnice (1.5), |
| tcl | teplota oděvu [°C], |
| hc | součinitel přestupu tepla prouděním (konvekcí) [W.m-2.K-1]; viz tab. 1, |
| ta | teplota vzduchu [°C], |
| AD | povrch lidského těla [m2]; podle DuBoise (1916) - viz rovnice (1.2), |
| m | hmotnost člověka [kg], |
| h | výška člověka [m], |
| Icl | tepelná izolace oděvu [clo]. |
Součinitel přestupu tepla sáláním (radiací)
se vypočte z rovnice [8]
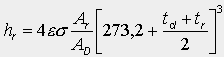(1.5)
kde:
| hr | součinitel přestupu tepla sáláním (radiací) [W.m-2.K-1], |
| ε | emisivita oděvu (pro běžný oděv téměř rovna 1; ε = 0,95 - Fanger (1967); ε = 0,98 - Gonzalez (1995)), |
| s | součinitel sálání černého tělesa s = 5,67.10-8 W.m-2.K-4, |
| Ar | povrch těla účastnící se výměny tepla sáláním [m2], |
| AD | povrch lidského těla [m2]; podle DuBois (1916) rovnice (1.2); (Ar/AD je pro sedící osoby = 0,7, pro stojící osoby = 0,73; Fanger (1967)), |
| tcl | teplota oděvu [°C], |
| tr | střední radiační teplota [°C]. |
Rovnici (1.1) není vždy možné explicitně vyřešit, poněvadž tcl je neznámá. Jistá forma iterace je poté nezbytná, je-li požadováno přesné řešení. Naštěstí součinitel přestupu tepla sáláním hr je pro typické teploty vnitřního prostředí a běžné oděvy téměř konstantní hodnota hr = 4,7 W.m-2.K-1. Jestliže je emisivita e výrazně nižší než 1, hodnota součinitele přestupu tepla sáláním hr by pak měla být upravena podle vztahu
hr = 4,7 ε (1.6)
kde ε vyjadřuje vážený průměr emisivit jednotlivých povrchů lidského těla.
Součinitel přestupu tepla prouděním (konvekcí)
Tepelný tok prouděním je způsobován prouděním vzduchu v místnosti nebo pohybem člověka. Součinitel přestupu tepla prouděním se vypočte pro různé okrajové podmínky různě; viz tab. 1. Všechny součinitele přestupu tepla v tab. 1 jsou stanoveny pro nebo velmi blízko tlaku 101,33 kPa. Tyto součinitele musí být tedy vždy upraveny pro konkrétní atmosférický tlak [8]:
hcc = hc (pt/101,33)0,55 (1.7)
kde:
| hcc | opravený součinitel přestupu tepla prouděním (konvekcí) [W.m-2.K-1], |
| pt | lokální atmosférický tlak [kPa]. |
Rovnici (1.1) lze též vyjádřit s použitím součinitele přestupu tepla konvekcí i radiací h a operativní teploty to:
R + C = fcl h (tcl - to) (1.8)
h = hr + hc (1.9)
odkud
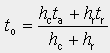(1.10)
kde:
| R | tepelný tok sáláním (radiací) [W.m-2], |
| C | tepelný tok prouděním (konvekcí) [W.m-2], |
| fcl | poměr povrchu těla pokrytého oděvem Acl a povrchu neoblečeného těla AD [-]; viz rovnice (1.4), |
| h | součinitel přestupu tepla konvekcí i radiací [W.m-2.K-1]; viz rovnice (1.9), |
| hr | součinitel přestupu tepla sáláním (radiací) [W.m-2.K-1]; viz rovnice (1.5), |
| hc | součinitel přestupu tepla prouděním (konvekcí) [W.m-2.K-1]; viz tab. 1, |
| to | operativní teplota [°C], |
| ta | teplota vzduchu [°C], |
| tr | střední radiační teplota [°C]. |
Operativní teplota je tedy váženým průměrem teploty vzduchu a střední radiační teploty podle odpovídajících součinitelů přestupu tepla konvekcí a sáláním.
| Rovnice | Limity | Podmínky | Poznámka/Zdroj |
|---|---|---|---|
| hc = 8,3 v0,6 hc = 3,1 |
0,2 < v < 4,0 0 < v < 0,2 |
sedící člověk + pohybující se vzduch | v je rychlost vzduchu [m.s-1] Mitchell (1974) |
| hc = 2,7 + 8,7 v0,67 hc = 5,1 |
0,15 < v < 1,5 0 < v < 0,15 |
ležící člověk + pohybující se vzduch | v je rychlost vzduchu [m.s-1] Colin a Houdas (1967) |
| hc = 8,6 v0,53 | 0,5 < v < 2,0 | procházející se člověk+ klidný vzduch | v je rychlost chůze [m.s-1] Nishi a Gagge (1970) |
| hc = 5,7 (M-0,8)0,39 | 1,1 < M < 3,0 | aktivní člověk + klidný vzduch | M je tep.produkce metabolismu [W.m-2] Gagge a kol. (1976) |
| hc = 6,5 v0,39 | 0,5 < v < 2,0 | neustále se pohybující člověk+ klidný vzduch | v je rychlost pohybu [m.s-1]Nishi a Gagge (1970) |
| hc = 14,8 v0,61 hc = 4,0 |
0,15 < v < 1,5 0 < v < 0,15 |
stojící člověk + pohybující se vzduch | v je rychlost vzduchu [m.s-1] Seppanen a kol. (1972) |
Tab. 1 - Rovnice pro výpočet součinitele přestupu tepla prouděním
2. STANOVENÍ OPERATIVNÍ TEPLOTY MĚŘENÍM
Pokud se operativní teplota stanovuje ve skutečném prostředí na základě měření fyzikálních veličin, jsou výchozími měřenými veličinami teplota kulového teploměru, teplota vzduchu a rychlost proudění vzduchu. Při rychlostech proudění vzduchu menších než 0,2 m.s-1 lze nahradit operativní teplotu výslednou teplotou kulového teploměru tg (°C). Při vyšších rychlostech existují vztahy pro výpočet operativní teploty z teploty vzduchu, teploty kulového teploměru a rychlosti proudění vzduchu.
2.1 Stanovení operativní teploty z teploty vzduchu ta, střední radiační teploty tr a rychlosti vzduchu var
Ve většině případů, kde je relativní rychlost proudění vzduchu malá (< 0,2 m.s-1) nebo kde je malý rozdíl mezi střední radiační teplotou a teplotou vzduchu (< 4 °C), je možno operativní teplotu vypočítat s dostatečným přiblížením jako aritmetický průměr teploty vzduchu ta a střední radiační teploty tr [1]. Při vyšších rychlostech vzduchu a větším rozdílu teplot ta a tr se operativní teplota určí z rovnice
to = A . ta + (1 - A) tr (2.1)
kde A je funkcí relativní rychlosti proudění vzduchu var [m.s-1] podle tab. 2.
| var [m.s-1] | 0,2 | 0,3 | 0,4 | 0,6 | 0,8 | 1,0 |
| A [-] | 0,50 | 0,53 | 0,60 | 0,65 | 0,70 | 0,75 |
Tab. 2 - Závislost koeficientu A pro výpočet operativní teploty to na rychlosti proudění vzduchu var [m.s-1]
2.2 Stanovení operativní teploty z teploty vzduchu ta, teploty kulového teploměru tg a rychlosti vzduchu va
Operativní teplotu lze též stanovit na základě znalosti výsledné teploty kulového teploměru tg, teploty vzduchu ta a rychlosti proudění vzduchu va z rovnice [7]
to = K . tg + (1 - K) ta (2.2)
kde:
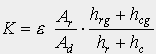(2.3)
| to | operativní teplota [°C], |
| ta | teplota vzduchu [°C], |
| tg | výsledná teplota kulového teploměru [°C], |
| K | váhový koeficient [-], |
| ε | emisivita kůže (oděvu) [-], |
 |
poměr sálajícího povrchu těla ku celkovému povrchu AD podle DuBois (1916) rovnice (1.2) [-], |
| hr | součinitel přestupu tepla sáláním (radiací) [W.m-2.K-1]; viz rovnice (1.5), |
| hc | součinitel přestupu tepla prouděním (konvekcí) [W.m-2.K-1]; viz tab. 1, |
| hrg | součinitel přestupu tepla sáláním v úrovni kulového teploměru [W.m-2.K-1]; viz rovnice (2.6), |
| hcg | součinitel přestupu tepla prouděním v úrovni kulového teploměru [W.m-2.K-1]; viz rovnice (2.4 a 2.5). |
Hodnoty součinitelů přestupu tepla sáláním a konvekcí v úrovni kulového teploměru se vypočítají z těchto rovnic [7]:
| - pro přirozené proudění vzduchu | hcg = 1,4 .(Δt/D)1/4 | (2.4) |
| - pro nucené proudění vzduchu | hcg = 6,3.(va0,5/D0,4) | (2.5) |
hrg = 6,01 W.m-2.K-1 (2.6)
kde:
| va | rychlost proudění vzduchu v úrovni koule [m.s-1], |
| D | průměr koule [m], |
| Δt | rozdíl teplot ta - tg [K]. |
V ideálním případě, kdy je K = 1, je operativní teplota to rovna výsledné teplotě kulového teploměru tg.
3. STANOVENÍ OPERATIVNÍ TEPLOTY MATEMATICKÝM MODELEM
Matematický model popisující operativní teplotu vychází z výše uvedeného základního vztahu (1.10). Model je možné vytvořit buď statický, který popisuje prostorové rozložení operativní teploty v jednom časovém okamžiku, nebo dynamický, který je schopen postihnout i časovou proměnu této hodnoty. Statický model je postačující pro řešení úloh typu "optimalizace rozmístění otopných ploch" nebo "stanovení extrémních podmínek v interiéru", zatímco dynamického modelu je vhodné použít na řešení úloh souvisejících s výpočty energetických ukazatelů a tepelné pohody objektů s přerušovaným vytápěním. Dynamický model je též vhodný pro simulaci chování inteligentních budov, kde operativní teplota v daném okamžiku a místě může být poruchovou veličinou pro zahájení činnosti automatické regulace.
Pro rychlosti do 0,2 m.s-1 je k výpočtu operativní teploty to postačující stanovení pouze teploty vzduchu ta a střední radiační teploty tr. Pro vyšší rychlosti proudění vzduchu je nutné již vzít v úvahu proudění a sestavování dynamického modelu operativní teploty vyžaduje již využití prvků CFD (Computational Fluid Dynamics) [5], [9].
3.1 Statické modelování
Statické modely slouží k základní orientaci v problému a používají se tam, kde je třeba "zmapovat" stav při určitém konkrétním navrhovaném řešení (např. rozmístění otopných ploch ve vytápěné místnosti) a na základě takto získané informace optimalizovat řešený problém. Neobsahují většinou žádné mechanismy pro popis chování budovy v čase za proměnných podmínek a pro popis interakce jednotlivých subsystémů budov.
|
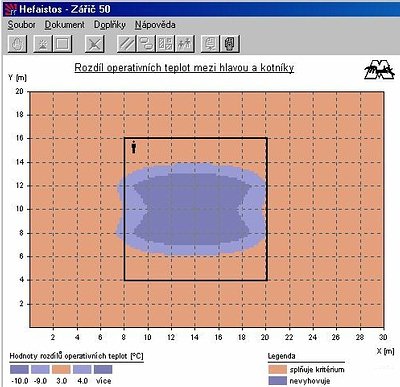
Obr. 1 - Grafický výstup z programu Hefaistos znázorňuje rozložení sálavého toku
a operativní teploty při podlaze haly. Patrný je vliv negativního sálání vratových otvorů
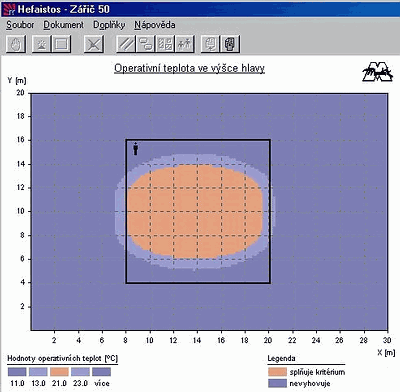
Obr. 2 - Grafický výstup z programu Hefaistos znázorňuje vyhodnocení splnění
hygienických požadavků podle 178/2001 Sb. na operativní teplotu ve výšce hlavy.
Patrné je nedosažení požadované operativní teploty u vrat
Příkladem statického modelu pro výpočet operativní teploty je program Hefaistos - Release 6. Fyzikální model, použitý v programu Hefaistos (Release 6), je uzpůsoben k popisu ustáleného stavu v uzavřených halách vytápěných především tmavými infrazářiči [10].
Pro účely výpočtu teploty vzduchu je hala horizontálně rozdělena na dolní a horní část ve výšce dané podle výkonu váženým průměrem výšek zavěšení všech infrazářičů. Teplota vzduchu je pak počítána vždy z energetického toku přes povrch haly na základě rovnováhy vnitřních tepelných zisků a tepelných ztrát haly. Výpočet neuvažuje zisky ze solárního záření.
Nejprve je teplota vzduchu vypočítána zvlášť pro dolní a horní část haly. Do dolní části je započtena dodávka energie zářením z infrazářičů, trvalý zisk tepla z technologií, ztráty odpovídající částí povrchu haly a infiltrace venkovního vzduchu. Do horní části je započten pouze přísun energie konvekcí z infrazářičů a ztráty odpovídající částí povrchu haly.
Pokud v horní části je teplota vzduchu vyšší, tak se zde trvale udržuje "polštář" teplého vzduchu a horizontální rozdělení haly je oprávněné. V dýchací zóně (1,5 m nad podlahou) je pak teplota vzduchu určena podle dolní části přepočtem na potřebnou výšku dle předpokládaného vertikálního rozvrstvení vzduchu s gradientem 0,3 K.m-1. Pokud však v horní části haly vyjde teplota vzduchu nižší, než teplota vzduchu ve spodní části haly (např. při špatné tepelné izolaci střechy), dochází ve skutečnosti k cirkulaci vzduchu mezi dolní a horní částí haly. Ve výpočtu je tato skutečnost zohledněna celým novým výpočtem bez uvažovaného horizontálního rozdělení haly.
Na základě znalosti teploty vzduchu jsou určeny i povrchové teploty jednotlivých obalových konstrukcí haly. Lze tak stanovit energii (dle záření absolutně černého tělesa), kterou povrch (jako plošný zdroj záření) vyzařuje zpět do haly. Operativní teplota v daném bodě uvnitř haly je tedy určena teplotou vzduchu a příspěvkem záření od všech infrazářičů i od celého povrchu haly. Pro výpočet operativní teploty se předpokládá rychlost proudění vzduchu menší než 0,2 m.s-1.
Vstupními údaji jsou požadovaná operativní teplota, geometrie haly, tepelně technické vlastnosti obvodových konstrukcí, provozní režim haly, teplotní oblast objektu, ve které se objekt nachází, požadavek na větrání, určení zóny pobytu lidí v hale a popis činnosti osob pobývajících v hale. Výstupem je grafické znázornění intenzity osálání a operativní teploty to v rovině zadané výšky nad podlahou (viz obr. 1) včetně hygienického posouzení, zda dané řešení vyhoví či nevyhoví hygienickým požadavkům. Jedním z požadavků je rozložení operativní teploty ve výšce hlavy (odpovídající poloze člověka - sedící/stojící) (obr. 2) a dalším pak rozdíl operativních teplot mezi hlavou a kotníky, podrobněji viz dále.
Toto hygienické vyhodnocení je znázorněno v půdorysném průmětu haly v zadané výšce. Tříbarevné mapy zobrazují oblasti, ve kterých jsou hygienické podmínky splněny (oranžová) nebo naopak nesplněny (tmavší odstín modré) a též tzv. toleranční pásmo, kde může být v určitých případech nesplnění kritéria ještě tolerováno (světlejší odstín modré). Pod každým průmětem je vždy legenda s hodnotami popisujícími jednotlivé barevné odstíny (viz obr. 2).
3.2 Dynamické modelování
Zjednodušené dynamické modely vycházejí především z regresní analýzy výsledků vícenásobného běhu statických modelů za různých okrajových podmínek. Tyto modely nejsou schopny postihnout charakteristiku přechodových dějů, jsou však schopny zohlednit chování budovy (systému) za různých podmínek.
Pro jednodušší systémy lze stanovit na základě okrajových podmínek matematickou funkci, popisující dynamickou odezvu systému. Existují dvě hlavní větve této metody - časová a frekvenční odezva.
Analogie mezi tepelnými a elektrickými obvody vede k aplikaci metod používaných v elektrických systémech na tepelné systémy. Tato metoda je výhodná především pro oblast základního výzkumu, neboť umožňuje poměrně v krátkém čase simulovat dlouhá období, zatím je však málo praktických aplikací.
Se zvyšujícími se výkony výpočetní techniky se stále více aplikují numerické metody. Pro modelování aktivních systémů se jako vhodná jeví metoda konečných diferencí a metoda konečných prvků. Metoda sítí je jedna z nejčastěji používaných v oboru modelování budov.
Jedním z dynamických modelů je ESP-r (Environmental Systems Performance; r - research) [5], [9]. ESP-r je simulační nástroj, který obsahuje mechanismy pro popis chování budovy v čase za proměnných podmínek a pro popis interakce jednotlivých subsystémů budov.
Nejprve je třeba sestavit počítačový model simulovaného objektu. Budova se rozdělí na nezbytně nutný počet zón, v závislosti na simulovaném problému. U každé zóny musí být zadána geometrie, skladba jednotlivých konstrukcí (je možné použít databázi konstrukcí, která je součástí programu a nebo vytvořit databázi novou) a činnosti, ke kterým v dané zóně dochází. Dále je možné v každé zóně zadat infiltraci a výměnu vzduchu mezi jednotlivými zónami, náhodné zisky, zastínění, žaluzie a rolety, data pro výpočet součinitelů osálání, přestupu tepla konvencí atd. Rovněž je možné zadat jednotlivé komponenty otopné soustavy a jejich propojení.
Výstupní hodnoty ESP-r jsou číselné a grafické (obr. 3). Není však možné obdržet grafické rozložení jednotlivých teplot v místnosti, lze jen zadat několik bodů, v kterých by tyto teploty měly být vyčísleny. Jde o výpočet na krychli (kvádru), jejíž rozměry jsou volitelné [11]. Chceme-li tedy obdržet hodnotu operativní teploty ve zvoleném místě, je třeba nejprve vypočítat střední radiační teplotu tr v tomto místě a teplotu vzduchu v místnosti ta. Operativní teplota je pak aritmetickým průměrem těchto hodnot za předpokladu rychlosti proudění vzduchu do 0,2 m.s-1.
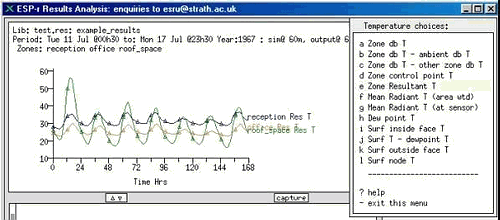
Obr. 3 - Grafický výstup z programu ESP-r - průběh operativní teploty v jednotlivých zónách modelu v čase
4. OPERATIVNÍ TEPLOTA JAKO KRITERIUM HODNOCENÍ TEPELNÉHO STAVU PROSTŘEDÍ
K vyhodnocení tepelného stavu vnitřního prostředí a následnému zajištění optimálního tepelného komfortu pro člověka je třeba stanovit několik parametrů, mezi něž patří i operativní teplota. Operativní teplota je tedy kriteriem pro hodnocení tepelné pohody prostředí. Optimální hodnoty operativní teploty jsou uvedeny v několika předpisech.
4.1 ČSN EN ISO 7730 Mírné tepelné prostředí - Stanovení ukazatelů PMV a PPD a popis podmínek tepelné pohody
ČSN EN ISO 7730 [1] je norma pro hodnocení tepelné pohody a popisuje, mimo jiné, podmínky tepelného mikroklimatu přijatelného pro tepelnou pohodu člověka. Mezi tyto podmínky patří i doporučené operativní teploty pro 90% spokojenost lidí v daném interiéru, které jsou patrné z tab. 3 a též z obr. 4, kde jsou znázorněny optimální operativní teploty (odpovídající PMV = 0) jako funkce tělesné aktivity a oděvu.
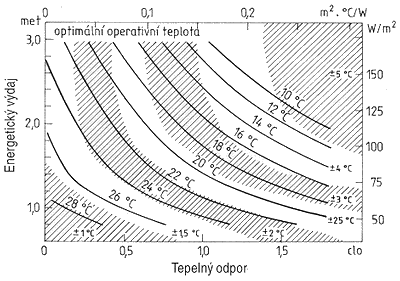
Obr. 4 - Optimální operativní teploty jako funkce tělesné aktivity a oděvu
| Období | Izolace oblečení [clo] |
Stupeň aktivity [met] |
Optimální operativní teplota [°C] |
Přípustné rozmezí operativní teploty [°C] |
|---|---|---|---|---|
| Zima | 1,0 | 1,2 | 22 | 20 až 24 |
| Léto | 0,5 | 1,2 | 24,5 | 23 až 26 |
Tab. 3 - Doporučené operativní teploty pro 90% spokojenost lidí v daném interiéru
4.2 Vládní nařízení č. 178/2001 Sb.
Tímto nařízením ze dne 18. 4. 2001 se stanoví podmínky ochrany zdraví zaměstnanců při práci a kromě jiného se stanoví i hygienické požadavky na pracovní prostředí a pracoviště [4]. Toto nařízení prochází v současné době (září 2002) revizí.
4.3 ANSI/ASHRAE 55-92 Thermal Environmental Conditions for Human Occupancy
Americká norma 55-1992 (Tepelné parametry interiéru obývaného člověkem) se zabývá tepelnou pohodou v interiérech, kde běžně pobývají lidé a uvažuje s 80% spokojeností osob pobývajících v daném interiéru [3]. Doporučené hodnoty operativní teploty pro dosažení celkové tepelné pohody, stanovené tímto předpisem, jsou uvedeny v tab. 4 a na obr. 5.
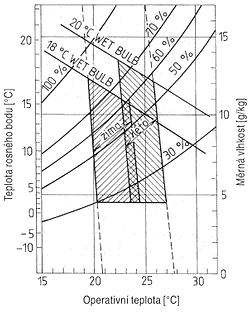
Obr. 5 - Přípustné rozmezí operativní teploty a vlhkosti vnitřního vzduchu
pro typické letní a zimní oblečení
wet bulb - teplota mokrého teploměru
| Období | Typické oblečení | Izolace oblečení [clo] |
Stupeň aktivity [met] |
Optimální operativní teplota [°C] |
Přípustné rozmezí operativní teploty [°C] |
|---|---|---|---|---|---|
| Zima | Silné kalhoty, košile s dlouhým rukávem a svetr |
0,9 | 1,2 | 22 | 20 až 23,5 |
| Léto | Slabé kalhoty, košile s krátkým rukávem | 0,5 | 1,2 | 24,5 | 23 až 26 |
| Minimální oblečení | 0,05 | 1,0 | 27 | 26 až 29 |
Tab. 4 - Optimální a přípustné operativní teploty pro osoby vykonávající lehkou práci, při relativní vlhkosti vzduchu 50% a střední rychlosti vzduchu ≤ 0,15 m.s-1
Metody počítačového modelování energetického chování systémů TZB a vnitřního prostředí jsou nepostradatelné pro optimalizaci systémů. Rozhodujícím prvkem v úspěšnosti aplikace těchto metod nejen v oblasti základního výzkumu ale i v praxi je volba vhodného modelu a detailu řešeného problému, kde musí být v souladu přesnost vstupních dat s požadovaným výstupem.
Tento příspěvek je součástí výzkumných záměrů CEZ J04/98: 210000005 a 21000011.
Literatura:
[ 1] ČSN EN ISO 7730, 1997. Mírné tepelné prostředí. Stanovení ukazatelů PMV a PPD a popis podmínek tepelné pohody. Český normalizační institut
[ 2] ČSN ISO 7726, 1993. Tepelné prostředí. Přístroje a metody měření fyzikálních veličin. Federální úřad pro normalizaci a měření
[ 3] ANSI/ASHRAE 55-1992. Thermal Environmental Conditions for Human Occupancy. American Society of Heating, Refrigerating and Air Conditioning Engineers, Atlanta
[ 4] Vládní nařízení č. 178/2001 Sb. ze dne 18. 4. 2001, kterým se stanoví podmínky ochrany zdraví zaměstnanců při práci. Sbírka zákonů ČR
[ 5] CLARKE, J., 1974-77. Simulační program ESP-r, část doktorské práce, University of Strathclyde, Glasgow
[ 6] ASHRAE, 2001. Fundamentals - Thermal Comfort. ASHRAE Handbook, chapter 8, American Society of Heating, Refrigerating and Air Conditioning Engineers, Atlanta
[ 7] ASHRAE, 1999. Applications - Radiant Heating and Cooling. ASHRAE Handbook, chapter 52, American Society of Heating, Refrigerating and Air Conditioning Engineers, Atlanta
[ 8] Sars G., Pernot C., de Wit M., 1988. ESPmrt, a new module for the ESP- system. University of Technology Eindhoven, Institute of Applied Physics TNO-TH, Eindhoven
[ 9] HENSEN, J. L. M., 1991. On the thermal interaction of building structure and heating and ventilating system. Doctoral dissertation Eindhoven University of Technology (FAGO)
[10] KABELE, K., PINKAS, P., HAKEN, 2000. Modelování a simulace energetických systému budov 4. Topenářství-instalace, 34, č. 5
[11] KRTKOVÁ, Z., KABELE, K.,2000. Možnosti využití simulačního programu ESP-r pro výpočet střední radiační teploty. Sborník 1. národní konference Simulace budov 2000, pp. 96-101, Praha, IBPSA CZ, 2000
[12] KABELE, K., KADLECOVÁ, M., KRTKOVÁ, Z.,2000. Application of the computer simulation in warm-air heating system design in low-energy buildings. Proceedings of the 4th international conference Energy for Buildings, pp 271-287, Vilnjus
[13] CENTNEROVÁ, L., 2001. Tradiční a adaptivní model tepelné pohody. Disertační práce, ČVUT v Praze
[14] FANGER, P.O., 1972. Thermal comfort. McGraw-Hill, New York.
