Má pára budoucnost? (II)
Parovody
Rozvody vodní páry (parovody) od zdroje ke spotřebičům mají vlastně za úkol přenos tepelné energie z místa její výroby do míst její spotřeby. Je tedy nutné omezit na minimum ztráty vyrobené tepelné energie a energii dopravit pokud možno s takovými parametry, s jakými byla vyrobena, případně se tomuto ideálu maximálně přiblížit.
Pro pohyb páry v parovodu není, na rozdíl od vodních tepelných sítí, potřeba přídavné energie, tj. není nutno dodáním elektrické energie zajišťovat práci dopravních čerpadel. Pára se pohybuje vlastním tlakem, který se však v průběhu přenosu páry snižuje vlivem tlakových ztrát v potrubí. V průběhu přenosu páry však dochází nejen k tlakovým, ale i k tepelným ztrátám v potrubí.
Tlakové ztráty úseku parního potrubí vycházejí z obecné Bernoulliho rovnice kontinuity a jsou dány součtem tlakových ztrát třením a tlakových ztrát způsobených vřazenými odpory v potrubí. Tedy platí obecně:
Δp = ∑ [(λi . Li . ρi . vi2 . (2d)-1] + ∑ [ζi . ρi . vi2 . 2-1]
kde:
| Δp | celková tlaková ztráta | [Pa] |
| λi | součinitel tření v potrubí i-tého úseku potrubí | [-] |
| Li | délka i-tého úseku potrubí | [m] |
| ρi | hustota páry v i-tém úseku potrubí | [kg . m-3] |
| vi | rychlost páry v i-tém úseku potrubí | [m . s-1] |
| d | vnitřní průměr i-tého úseku potrubí | [m] |
| ζi | součtový součinitel místních ztrát i-tého úseku potrubí | [-] |
Prakticky lze však s úspěchem pro stanovení tlakových ztrát jednotlivých úseků parního potrubí použít nomogram, zpracovaný před více než čtvrt stoletím, který lze získat od starších kolegů. Je sice zpracován ve starých jednotkách, ale obecně je stále platný pro tlakové ztráty třením. Rovněž lze použít nomogram, uvedený v sešitu projektanta č. 9 (vydání STP - 2001) - Laboutka, Suchánek - "Výpočtové tabulky pro vytápění", strana č. 91. Pro zahrnutí tlakových ztrát vřazenými odpory se celková součtová tlaková ztráta potrubí třením zvýší podle dobové literatury o 5 až 10 %, podle délky a složitosti parního potrubí.
Vlivem tlakových ztrát parovodu dochází k poklesu tlaku páry, entalpie páry zůstává nezměněna, podobně jako při redukci tlaku páry. Pokud by nedocházelo k tepelným ztrátám potrubí, pára v potrubí by se přehřívala - konkrétní hodnoty lze odečíst z parních tabulek.
Vlivem tepelných ztrát v potrubí dochází k úbytku tepelného obsahu, tedy entalpie páry.
Podíl úbytku entalpie a tlakových ztrát se nazývá ztrátový poměr:
f = Δp . Δh-1
kde:
| f | ztrátový součinitel | [J . kg-1 . Pa-1] |
| Δp | celková tlaková ztráta | [Pa] |
| Δh | rozdíl entalpií páry | [J . kg-1] |
Z diagramu h-s (h - entalpie [kJ . kg-1], s - entropie - [kJ . kg-1 . K-1]) lze odečíst mezní ztrátový součinitel fm, jehož průběh pro různé vnitřní průměry potrubí je znázorněn na obrázku č. 1. Při rychlostech páry v potrubí právě na mezní rychlosti vm je pára proudící sytá, při rychlostech v potrubí nad vm se proudící pára přehřívá, při rychlostech v potrubí pod vm je proudící pára mokrá (definice stavů viz první část série).
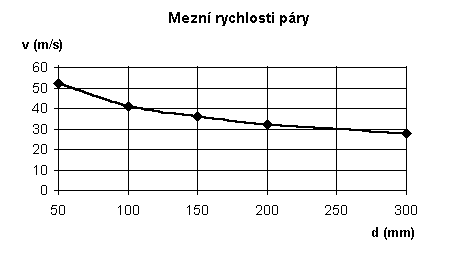
Obr. č. 1
Tepelné ztráty parního potrubí lze vyjádřit, při zavedení určitých zjednodušujících předpokladů - DN potrubí 50 až 300 mm, vnější průměr tepelné izolace je roven dvojnásobku vnějšího průměru potrubí, teplota v kanálu parovodu je konstantní (např. 30 °C) - následujícím vztahem:
Qp = q1 . Δt . I = 0,43 . Δt . I
kde:
| Qp | tepelná ztráta potrubí | [W] |
| q1 | měrná tepelná ztráta potrubí o délce 1 m, při rozdílu teplot páry a okolí 1 K | [W . m-1 . K-1] |
| Δt | rozdíl teplot páry a okolí | [K] |
| I | délka potrubního úseku | [m] |
Při těchto tepelných ztrátách bude v daném úseku potrubí vznikat kondenzát v množství:
mp = Qp . r-1
kde:
| mp | průtokové množství kondenzátu | [kg . h-1] |
| Qp | tepelná ztráta potrubí | [W] |
| r | měrné výparné teplo při tlaku páry v daném úseku potrubí | [Wh . kg-1] |
Uvedené vztahy však platí pouze pro nové potrubí s kvalitní tepelnou izolací. Pro staré potrubí s tepelnou izolací, jejíž objem se zmenšil, případně její vnější průměr neodpovídá daným předpokladům a při snížené rychlosti páry v potrubí (např. v létě), může být měrná tepelná ztráta a tím i tepelné ztráty a následně vzniklé množství kondenzátu i desetkrát vyšší. Pro praktické určení přibližného množství vznikajícího kondenzátu v 1 m potrubí DN 50 až 300 za výše uvedených podmínek je možno použít obrázek č. 2, kde je uvedena závislost množství vznikajícího kondenzátu na teplotě protékající páry.
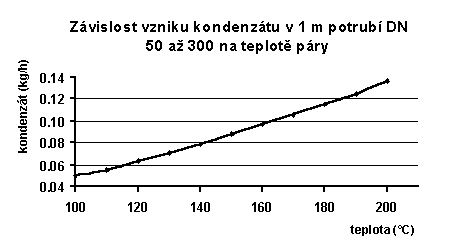
Obr. č. 2
Kondenzát, vzniklý v potrubí je nutno odvádět. Proto by parovod měl být po určitých vzdálenostech opatřen odváděcími soupravami. Příklad takové soupravy viz obrázek č. 3. Označení P - parovod, K - kondenzát.
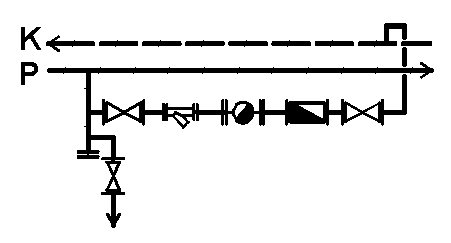
Obr. č. 3
Kondenzát z parovodu má teplotu jen o málo nižší, než je teplota páry v parovodu. Proto je v některých případech (např. u plastových kondenzátních potrubí) nutno použít chladiče kondenzátu. Typy odvaděčů kondenzátu a vhodnost jejich použití, budou popsány ve čtvrtém pokračování této série.
V důsledku nízké objemové hmotnosti páry se v našich podmínkách obvykle volí rychlost páry v potrubí v rozmezí 20 až 50 m . s-1. Čím větší průměr potrubí, tím vyšší rychlost je možno volit. V literatuře jsou zmínky o podstatně vyšších rychlostech v parovodech (dokonce až 366 m/s), které by mohly přinést podstatné zvýšení "propustnosti" parovodů, bylo by ovšem nutno nejprve prokázat výhody a nevýhody takovýchto rychlostí (životnost potrubních sítí oproti nižším nákladům na potrubí na jednotku přepravené energie, úbytek stěn potrubí za časovou jednotku a z toho plynoucí hospodárná síla stěny potrubí, přehřátí páry v místě spotřeby a z toho plynoucí náklady na spotřebič apod.). Technicky by vysoké rychlosti v přepravním parním potrubí určitě řešitelné byly.