Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Teplotní exponent otopných těles

prof. Ing. Jiří Bašta, Ph.D., Ing. Jindřich Boháč, Ph.D.

Recenzovaný

Norma EN 442-2 předpokládá lineární závislost teplotního exponentu na výšce deskového otopného tělesa. Závislost však není lineární pro daný typ otopného tělesa, jak ukazuje vyhodnocení dat od výrobců.

Článek se zamýšlí nad normou EN 442-2 předpokládající lineární průběh teplotního exponentu s výškou pro daný typ otopných těles. Je zaměřen především na desková otopná tělesa, i když nepomíjí ani ostatní druhy otopných těles. Na základě vyhodnocení nashromážděných dat od výrobců otopných těles poukazuje na skutečnost, že závislost teplotního exponentu na výšce není pro daný typ otopného tělesa lineární a s výškou rostoucí, jak předpokládá charakteristická rovnice typu.

Úvod

Teplotní exponent otopných těles se určuje experimentálně pro každý druh, typ otopných těles, resp. pro dané otopné těleso v laboratorních podmínkách podle ČSN EN 442-2 a nelze jej tedy jednoduše vypočítat. Opakovaným měřením tepelného výkonu téhož otopného tělesa při různých teplotních parametrech se získají potřebné údaje pro výpočet teplotního exponentu regresní metodou nejmenších čtverců pro jeden vzorek.

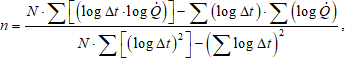
kde je

N: počet měření výkonu při různých teplotních parametrech [–],
Q: naměřený tepelný výkon [W],
Δt: teplotní rozdíl, tj. ochlazení vody na tělese [K].

Norma víceméně u daného typu otopného tělesa zanedbává vliv délky otopného tělesa L na teplotní exponent a vliv výšky tělesa H uvažuje lineární ve smyslu zápisu charakteristické rovnice typu. Jinými slovy závislost teplotního exponentu na výšce otopného tělesa je vyjadřována rovnicí přímky [1].

Teoretické předpoklady dané ČSN EN 442-2

Charakteristická rovnice, vyjadřující tepelný výkon ve tvaru funkce teplotního rozdílu, a zároveň mocninné funkce s teplotním exponentem nás upozorňuje na skutečnost, že vývoj teplotního součinitele s výškou lze považovat rovněž za lineární.

Obecný tvar charakteristické rovnice typu pro tepelný výkon otopného tělesa vypadá následovně.

kde je

L: délka otopného tělesa [m],
H: výška otopného tělesa [m],
ṁ_w: hmotnostní průtok vody tělesem [kg/s],
Δt: rozdíl teploty přívodní a vratné vody [K],
c₀: výškový posun [–],
c₁: směrnice přímky [–],
a, b, c, K_T: experimentálně získané konstanty [–].

Parametry, které jsou v průběhu měření jednoho vzorku, tj. otopného tělesa, konstantní vyřadíme z obecného tvaru rovnice a dostaneme velmi jednoduchý tvar normativní charakteristické rovnice pro měřené otopné těleso (s výjimkou konvektorů). Tato rovnice je tak validní pro měření jednoho zkušebního vzorku.

kde je

K_M: konstanta vzorku [–],
n: teplotní exponent OT [–].

Vidíme tedy exponenciální rovnici, kde exponent n je teplotním exponentem otopného tělesa, který je nesmírně důležitý v praxi pro další přepočty tepelných výkonů otopných těles. Charakteristická rovnice typu (typ, tzn. např. deskové otopné těleso typu 10, typu 11 atd.) bude mít níže uvedený tvar.

kde je

K_T: pro daný typ tělesa experimentálně zjištěná konstanta [–].

Teplotní exponent tedy vystupuje jako lineární funkce výšky H otopného tělesa ve tvaru:

V praxi se však závislost na výšce otopného tělesa projevuje většinou skrytě, neboť výrobci udávají teplotní exponent n pro výrobní řadu určitého typu otopných těles s určitou výškou H, a právě tyto hodnoty uváděné výrobci, tj. převzaté od zkušeben, byly shromážděny pro vyhodnocení v literatuře [2].

Charakteristická rovnice typu v obecném tvaru je vlastně regresní rovnicí typu, což je rovnice umožňující výpočet jmenovitého tepelného výkonu a teplotního exponentu všech těles daného typu jako funkci charakteristického rozměru, v našem případě výšky otopného tělesa.

Níže uvedený graf zobrazuje závislost teplotního exponentu na výšce jednotlivých typů deskových otopných těles [3]. Je evidentní, že prof. Hahn vyšel ve své studii z předpokladu normy a nezjišťoval skutečné, experimentálně zjištěné hodnoty teplotních exponentů různě vysokých otopných těles (OT) daného typu, neboť vyznačil pouze široké pásmo s lineárním průběhem o jednotné směrnici pro jednotlivé typy deskových otopných těles. Další obrázky vycházející z nashromážděných dat tak s úspěchem mohou graf na obr. 1 vyvrátit.

Obr. 1 Závislost teplotního exponentu n na výšce deskových otopných těles H [3]

Co představuje teplotní exponent?

Teplotní exponent je určen experimentálně, tj. je vypočten z naměřených hodnot v měřicí komoře pro příslušné otopné těleso. Jestliže dosadíme např. čtyři výkony téhož tělesa do závislosti na Δt a proložíme jimi v logaritmických souřadnicích přímku, bude její směrnice představovat hodnotu teplotního exponentu n. Je tedy zřejmé, že n závisí jak na druhu či typu tělesa, tak na průtoku (hlavně u konvektorů), ale bohužel i na teplotách a dalších konstrukčních rozměrech. Teplotní exponent se však v rámci výpočtů pro příslušný typ otopného tělesa uvažuje jako konstantní.

Již bylo uvedeno, že tepelný výkon otopného tělesa

je dán jeho teplosměnnou plochou S_L, součinitelem prostupu tepla k a rozdílem střední teploty vody t_wm a okolního vzduchu v definičním bodě t_D. Jmenovité (normované – index n) podmínky představují: t_w₁_n = 75 °C, t_w₂_n = 65 °C, t_D = 20 °C (tj. v podobě obvyklého zápisu 75/65/20 °C).

Jestliže se výkon změní, bude velikost jeho změny dána poměrem skutečného a jmenovitého tepelného výkonu. S úspěchem můžeme tuto změnu popsat rovnicemi vyjadřujícími prostup tepla stěnou otopného tělesa z otopné vody do vytápěného prostoru.

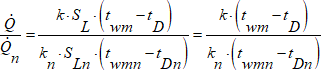
Podíváme-li se na tuto rovnici, můžeme z ní okamžitě vykrátit přestupní plochu, neboť u daného vzorku otopného tělesa zůstává přestupní plocha stále stejná S_L = S_Ln. Problémem je však změna součinitele prostupu tepla k/k_n, neboť v součiniteli prostupu tepla jsou zahrnuty součinitele přestupu tepla na straně vody a vzduchu, které se určují z kriteriálních rovnic s velikou nepřesností. Řešením je nahradit změnu součinitele prostupu tepla exponenciální funkcí a exponent určovat experimentálně pro dané otopné těleso. Tak jsme získali teplotní exponent otopného tělesa n pro přepočet výkonů otopných těles na jiné teplotní parametry. Teplotní exponent otopných těles vlastně představuje změnu součinitele prostupu tepla otopných těles se změnou teplotních parametrů.

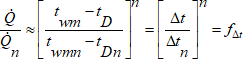
Vyhodnocení nashromážděných dat

V práci [2] byly zjišťovány hodnoty teplotních exponentů všech druhů a typů deskových otopných těles z katalogů od největších dodavatelů otopných těles. Sortiment, nabízený dodavateli je velmi široký, nicméně z teorie víme, že by se teplotní exponent deskových otopných těles měl lineárně zvětšovat se zvyšující se konstrukční výškou. Zjištěné údaje však této teorii ne vždy odpovídají, jak nám ukazuje obr. 2 pro deskové OT typu 10.

Obr. 2 Závislost teplotního exponentu n na výšce H otopného tělesa typu 10 [2]

Pro otopné těleso typu 10 vykazují firmy Purmo a Korado vyšší teplotní exponent oproti firmám Korad a Kermi. U společnosti Kermi, jako jediné z výběru, vidíme nárůst velikosti teplotního exponentu, který se „láme“ v 600 mm konstrukční výšky. U ostatních dochází v tomto „bodě“ naopak ke zvýšení. Nejvyšší hodnotu teplotního exponentu můžeme nalézt u firmy Purmo. Zaměříme-li se na typ 10, vidíme, že průběh teplotního exponentu odporuje základním teoretickým předpokladům přijatým pro měření otopných těles v kalorimetrických komorách. V ČSN EN 442-2 se jednoznačně vychází ze závěru, že teplotní exponent je dán lineární funkcí v celém rozsahu výšky daného typu otopného tělesa a pro různé typy a druhy otopných těles se mění pouze výškový posun a směrnice přímky. Pokud se podíváme na obr. 2, který vychází z dat prezentovaných výrobci, je patrné, že pro typ 10 není splněna podmínka lineární funkce teplotního exponentu s výškou otopného tělesa.

Tato nesrovnalost v rámci teoretického předpokladu průběhu teplotního exponentu na výšce otopného tělesa s reálně dosaženými hodnotami, může být dána u otopného tělesa typu 10 měnícím se podílem sálavé a konvekční složky s výškou právě u této jednoduché desky. Můžeme vidět, že průběh teplotního exponentu plně odpovídá teoretické lineární závislosti až u těles vyšších než 600 mm. Teoretických předpokladů začínají postupně dosahovat až typy deskových otopných těles s více deskami a rozšířenou přestupní plochou, tj. 11 až 33.

Obr. 3 Závislost aproximovaných hodnot teplotního exponentu n všech typů deskových otopných těles na výšce H [2]

Obr. 3 zabývající se deskovými otopnými tělesy zobrazuje aproximované hodnoty teplotního exponentu n, jakožto lineární funkce v závislosti na konstrukční výšce H. Tyto křivky zobrazují zprůměrované hodnoty teplotního exponentu pro příslušné typy deskových otopných těles od výšky 300 do 900 mm od všech vybraných výrobců vyjma firmy Kermi pro typ 21. V rámci technických podkladů této firmy nebyly dohledány teplotní exponenty pro otopná tělesa typu 21. Průběhy proložených hodnot, až na deskové otopné těleso typu 10, nám potvrzují splnění teoretického předpokladu dle ČSN EN 442-2.

Z grafu je patrné, že zvětšováním výšky otopných těles dochází k lineárnímu zvětšování teplotního exponentu deskového otopného tělesa, byť s jinou směrnicí pro jednotlivé typy. Opačného efektu dosahujeme u otopného tělesa typu 10 až do výšky 600 mm, čímž se dostáváme do rozporu s teoretickým předpokladem. Tato skutečnost nám říká, že se zvětšením konstrukční výšky dostáváme proměnlivé hodnoty tepelného výkonu sdíleného sáláním a konvekcí, které po zprůměrování a aproximování lineární funkcí ve výsledku klesají až do určité typické výšky otopného tělesa. V tomto bodě dochází ke zlomu, resp. ke zvýšení teplotního exponentu pro desková otopná tělesa typu 10.

Obr. 4 Závislost teplotního exponentu n článkového otopného tělesa ATOL na výšce H [2]

Přehled závislosti teplotního exponentu pro článková otopná tělesa Atol na výšce tělesa H a hloubce článku B můžeme vidět na obr. 4, kde například článkové otopné těleso ATOL o hloubce článku 189 mm dosahuje nejvyšší hodnoty teplotního exponentu při výšce 1730 mm [2].

U článkových otopných těles o hloubce 66 a 148 mm dochází k pomalému nárůstu teplotního exponentu v závislosti na zvětšení výšky. Naopak pro tělesa o hloubce 189 mm a 230 mm dochází nejprve k poklesu a až následně k růstu. U článkových otopných těles o hloubce 189 mm dochází k dalšímu zlomu a následnému poklesu při výšce 1730 mm. Otopná tělesa o hloubce článku 107 mm mají víceméně konstantní hodnotu teplotního exponentu až do výšky 930 mm. Poté teplotní exponent vykazuje rostoucí a opět klesající trend. U článkových otopných těles tak nelze hovořit o splnění teoretického předpokladu, že teplotní exponent s výškou otopného tělesa roste.

V práci [2] byly nashromážděny informace i pro nástěnné a podlahové konvektory, u kterých je tato problematika složitější o vliv průtoku a hloubky skříně konvektoru. U nástěnných konvektorů o malé hloubce můžeme dokonce pozorovat opačný trend vývoje teplotního exponentu (záporná směrnice) s výškou skříně konvektoru a u hloubky skříně konvektoru nad 100 mm již odpovídající předpokladům. U podlahových konvektorů dostáváme velmi proměnný a nestálý trend vývoje teplotního exponentu s výškou skříně konvektoru v rozmezí 90 až 300 mm.

Závěr

Hodnoty teplotních exponentů, které byly interpretovány v grafech, ukazují menší či větší odchýlení od lineárního průběhu teplotního exponentu s výškou otopného tělesa.

Téměř pro všechny typy deskových otopných těles platí rostoucí průběh teplotního exponentu, který víceméně odpovídá teoreticky očekávaným hodnotám. Výjimkou se v rámci jednotlivých typů deskových otopných těles stává deskové otopné těleso typu 10, u kterého se předpokládaný průběh nepotvrdil. Tato výjimka by se dala objasnit podrobnější experimentální studií diskutující vliv podílu sálavé a konvekční složky tepelného výkonu na teplotní exponent s rostoucí konstrukční výškou otopných těles. Jinými slovy, je otázkou, zda do určité výšky prosté desky neroste sálavá složka výkonu otopného tělesa rychleji, než jeho konvekční složka. Tento předpoklad vychází z poznatku, že čím je vyšší teplotní exponent u jednotlivých druhů otopných těles, tím větší podíl přirozené konvekční složky vykazují. Aproximované hodnoty teplotního exponentu v závislosti na výšce tělesa (viz obr. 3) nám poskytují další informace o vlastnostech deskových otopných těles. Ideálně splňující teoretický předpoklad pro lineární růst teplotního exponentu s výškou otopného tělesa získáme u deskových otopných těles typu 33.

Nízké hodnoty exponentu se projevují u deskových otopných těles bez konvekčních plechů. Především pak u typu 20, ale i typu 30, který je rozměrově náročnější a má menší průměrnou hodnotu teplotního exponentu nežli typ 21 a 22. Tento fakt vychází ze specifického použití otopných těles bez konvekčního plechu s větší konstrukční hloubkou, mnohdy i bez krycí mřížky a bočnic, s ohledem na vytápění objektů se zvýšeným požadavkem na hygienu a potřebou pravidelného otírání dezinfekcí.

U konvektorů získáváme velmi proměnlivé hodnoty, a to jak pro konvektory bez ventilátoru, tak i s ventilátorem. Nelze tedy jednoznačně uvést, jak se budou konvektory s přirozeným vybíjením tepla chovat pouze s ohledem na vývoj teplotního exponentu a výšky skříně konvektoru. Zde by bylo nutné sledovat rovněž hloubku skříně konvektoru, hmotnostní průtok a event. mezeru mezi žebrovkou a skříní konvektoru s ohledem na obtékání, resp. protékání žebrovky. Jinými slovy, bylo by nutné zahrnout mnohem více konstrukčních parametrů s ohledem na vývoj teplotního exponentu než pouze výšku H. Je zřejmé, že konvektory nesplňují předpoklad ČSN EN 442-2, že teplotní exponent s konstrukční výškou lineárně roste.

Článková otopná tělesa od výšky 230 do 2430 mm mají vyhovující hodnoty teplotního exponentu z pohledu předpokladů vývoje n podle ČSN EN 442-2. Rovněž však zde hraje neopominutelnou roli hloubka článkových otopných těles.

Problematika teplotního exponentu se týká i trubkových koupelnových otopných těles. Avšak s ohledem na širokou variabilitu otopné plochy tohoto druhu těles nelze jednoznačně předpokládat vývoj teplotního exponentu pouze s výškou tělesa.

Předpoklady dané ČSN EN 442-2 stran lineárního vývoje teplotního exponentu s rostoucí výškou daného typu otopného tělesa nebyly zdaleka vždy splněny. Je tedy otázkou, zda by tato lineární funkce závislá na jediném konstrukčním parametru, tj. výšce, neměla být pro daný typ otopných těles nahrazena jinou funkcí. Funkcí zahrnující alespoň dva konstrukční parametry, např. výšku H a hloubku B otopného tělesa.

Teplotní exponent je určován experimentálně v akreditovaných laboratořích a výrobci otopných těles mají povinnost takto určené teplotní exponenty uvádět. Proto bylo vycházeno z teplotních exponentů uváděných výrobci, aniž byly jakkoli zpochybňovány.

Použitá literatura

Bašta, J.: Otopné plochy – otopná tělesa. Praha: Ediční středisko ČVUT, 2016. – 204 s. – ISBN 978-80-01-05943-2.
Slavík, V.: Teplotní exponent otopných těles. ČVUT v Praze, FS. BP 2020. 5-TZSI-2020
Gebäudeplanung: Auslegung von Heizungsanlagen [online]. Fachhochschule Dortmund, 2012.
ČSN EN 442-2 Otopná tělesa – Zkoušky a jejich vyhodnocování.
Volně přístupné firemní podklady na www

Článek je převzat z časopisu VVI se souhlasem redakce.

English Synopsis

Temperature exponent of radiators

The article considers the standard EN 442-2, which assumes a linear course of the temperature exponent with height for a given type of radiators. It focuses mainly on panel radiators, although it does not omit other kinds of radiators. It points to the fact that the dependence of the temperature exponent on height is not linear and increasing for a given type, as assumed by the characteristic equation of the type. Results are based on the evaluation of the data collected from the radiator manufacturers.