Co znamená veličina NPSH pro oběhová čerpadla?
Výrobci odstředivých oběhových čerpadel uvádějí v projektových podkladech průběh hodnot veličiny nazývané NPSH. V příspěvku si vysvětlíme, co tato veličina představuje a k čemu slouží v topenářské praxi při návrhu oběhových čerpadel (OČ) do tepelných soustav.
Úvod
Hlavní podmínkou pro bezvadnou funkci oběhového čerpadla je zajištění dostatečného statického tlaku v čerpadle, zejména v jeho sací části. V čerpadle se urychluje voda, a proto klesá statický tlak. Nesmí však klesnout pod tlak nasycených par, což by znamenalo místní odpařování vody a vznik kavitace. Při kavitaci se odpařuje voda a vznikají bublinky vodní páry. Také dochází k vylučování plynů, zejména vzduchu, které jsou ve vodě rozpuštěny. Kavitací se snižuje hydraulická účinnost čerpadla a v čerpadle může docházet k hluku. V místě zániku kavitačních bublin také může docházet k opotřebování lopatek oběžného kola.
V příspěvku je u statického tlaku rozlišován pojem tlak a přetlak. Tlakem je míněn tlak absolutní, ne přetlak.
Hydraulické poměry v oběhovém čerpadle
Nejprve se seznámíme s hydraulickými poměry v sací části oběhového čerpadla. V této části dochází k největšímu snížení statického tlaku vody. Následně stanovíme požadované tlakové poměry v sání oběhového čerpadla, při kterých bude zajištěno, že voda proudící čerpadlem bude vždy v kapalném skupenství. V čerpadlové technice je hlavní veličinou pro energetické výpočty měrná energie čerpadla Y (J . kg-1). V tepelné technice je výhodnější pro energetické úvahy kolem oběhových čerpadel používat tlak a tlakový rozdíl. Převod mezi měrnou energií čerpadla Y (J . kg-1) a tlakovým rozdílem (přínosem) na čerpadle Δp (kPa) je dán vztahem
Δp = 10-3 . ρ . Y,
kde ρ je hustota vody při dané teplotě (tab. 1) (kg . m-3).
Orientačně platí, že Δp (kPa) ≈ Y (J . kg-1), protože hustota studené vody je přibližně 103 kg . m-3.
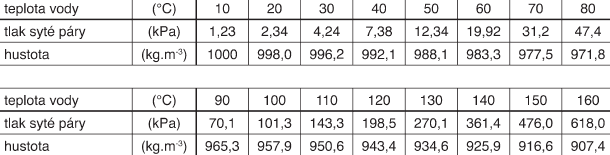
Tab. 1 - Základní vlastnosti vody
Při vtoku vody do oběhového čerpadla (obr. 1) vstupuje voda nejprve do sacího hrdla (1) a potom je přisávána k lopatkám oběžného kola (2). Těsně před vstupem do lopatek, kdy voda není ještě oběžným kolem unášena a kdy není statický tlak oběžným kolem zvyšován, je dosaženo minima statického tlaku vody v čerpadle. Pro proudění vody mezi místy 1 a 2 platí Bernoulliho rovnice o zachování energie daná rovností celkových tlaků neboli rovností součtu tlakových složek v uvedených místech
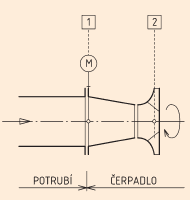 Obr. 1 - Schéma nátoku čerpadla |
ps1 + pb + pd1 = ps2 + pb + pd2 + Δpz, (1)
kde
ps1 je statický přetlak v sacím hrdle OČ (kPa)
pb - barometrický tlak (kPa)
pd1 - dynamický tlak v sacím hrdle OČ (kPa)
ps2 - statický přetlak před oběžným kolem OČ (kPa)
pd2 - dynamický tlak před oběžným kolem OČ (kPa)
Δpz - tlaková ztráta mezi místy 1 a 2 (kPa).
Protože veličiny ps2, pd2 a Δpz nelze v místě (2) čerpadla měřit přímo, zaveďme, že
Δpe = pd2 + Δpz, (2)
kde Δpe (kPa) je pokles tlakové energie v sací části čerpadla.
Z definice Δpe ve vztahu (2) vyplývá, že pokles tlakové energie v sací části čerpadla je dán součtem dynamického tlaku pd2 a tlakové ztráty Δpz v místě (2). Protože oba členy ve vztahu (2) závisí na druhé mocnině průtoku, je patrné, že pokles tlakové energie v sací části čerpadla je také závislý na druhé mocnině průtoku. Pokud zavedeme, že statický tlak v místě (2) bude roven alespoň tlaku vodní páry na mezi sytosti při teplotě protékající vody, bude
ps2 + pb = pp, (3)
kde pp - tlak vodní páry na mezi sytosti při teplotě proudící vody (tab. 1) (kPa).
Potom lze vztah (1) upravit na tvar
ps1 + pb + pd1 = pp + Δpe, (4)
ze kterého lze vyjádřit minimální statický přetlak v sacím hrdle čerpadla (kPa), čili v místě (1), vztahem
ps1m = pp + Δpe - pb - pd1. (5)
Dynamický tlak v sacím hrdle OČ
pd1 = 5 . 10-4 . v12 . ρ, (6)
kde
v1 je rychlost vody v sacím hrdle (m . s-1)
ρ - hustota vody při dané teplotě (kg . m-3).
Po dosazení vztahu (6) do vztahu (5) dostáváme konečný vztah pro minimální statický přetlak v sacím hrdle čerpadla
ps1m = pp + Δpe - pb - 5 . 10-4 . v12 . ρ. (7)
Samozřejmě platí, že provozní statický přetlak v sacím hrdle čerpadla ps1 (kPa) musí vyhovovat podmínce
ps1 ≥ p1sm.
Jedni výrobci čerpadel doporučují, aby provozní přetlak v sacím hrdle čerpadla byl alespoň o 5 kPa vyšší než požadovaný minimální statický přetlak v sacím hrdle. Druzí zase doporučují, aby se k hodnotě Δpe přidalo 15 %. Tyto rezervy mají zajistit určitou jistotu s ohledem na kolísání přetlaku v tepelné soustavě. Je vhodné stanovit provozní přetlak tak, aby vyhovoval vyššímu z doporučovaných navýšení.
Hodnoty dynamického tlaku jsou u oběhových čerpadel pro tepelnou techniku v rozsahu 0,5 kPa (pro rychlost vody v1 = 1 m . s-1) až 50 kPa (pro v1 = 10 m . s-1).
Hodnoty Δpe se zjisťují na měřicí trati s čerpadlem pomocí změřených hodnot ps1 a následným výpočtem pomocí vztahu
Δpe = ps1 - pp + pb + 5 . 10-4 . v12 . ρ. (8)
Při měření se postupně snižuje přetlak v sacím hrdle, přičemž se sleduje stav, kdy dojde ke snižování Δp v charakteristice oběhového čerpadla vlivem snižování hydraulické účinnosti. Při tomto stavu se ze vztahu (8) vypočítá Δpe.
Co znamená NPHS?
V anglické a německé literatuře se pro určení dostatečného tlaku v čerpadle používá veličina NPSH (Net Positive Suction Head) s rozměrem (m), což představuje pokles tlakové energie v sací části čerpadla daný výškou vodního sloupce. Průběh hodnot veličiny NPSH čerpadla, tj. její závislost na průtoku vody čerpadlem, je většinou pro větší čerpadla uváděn v podkladech výrobce společně s charakteristikou čerpadla (obr. 2), průběhem elektrického příkonu P2 a s průběhem hydraulické účinnosti η (eta) (%). Charakteristikou čerpadla se rozumí závislost Δp = f (V), kde V (m3 . h-1) je objemový průtok. Výrobci často ještě uvádějí charakteristiku čerpadla jako závislost H = f (Q), kde H (m) je dopravní výškou a Q (m3 . h-1) objemovým průtokem.
Citované charakteristiky a průběhy (obr. 2) jsou zpracovány pro referenční teplotu vody 20 °C. Proto budou dále všechny veličiny, které jsou udávány při referenční teplotě vody 20 °C, označeny indexem r.
Převod mezi veličinou NPSH (m) čerpadla a poklesem tlakové energie v sací části čerpadla Δper (kPa) při referenční teplotě je dán vztahem
Δper = 10-3 . ρ . g . NPHS, (9)
kde g = 9,81 je zemské zrychlení (m . s-2).
Přitom platí, že Δper (kPa) ≈ 10 . NPHS (m).
Pokud jsou odečítány parametry čerpadla z jeho charakteristik, musí se vycházet z objemového průtoku vody při referenční teplotě. Referenční průtok (m3 . h-1) je dán vztahem
Vr = V. ρ / ρr, (10)
kde
V je objemový průtok vody při skutečné teplotě vody (m3 . h-1)
ρ - hustota vody při skutečné teplotě (kg . m-3)
ρr - hustota vody při referenční teplotě (kg . m-3).
V charakteristikách čerpadel jsou pro určitý průtok uváděny i rychlosti vody v sacím i výtlačném hrdle. Tato rychlost samozřejmě platí pro referenční teplotu vody. Rychlost vody v1 (m . s-1) při skutečné teplotě vody bude dána vztahem
v1 = v1r . ρr / ρ, (11)
kde v1r je referenční rychlost vody (m . s-1).
Pro stanovení minimálního statického přetlaku v sacím hrdle čerpadla je nutné ještě určit pokles tlakové energie v sací části čerpadla při skutečné teplotě vody. Skutečný pokles tlakové energie v sací části čerpadla (kPa) je dán vztahem
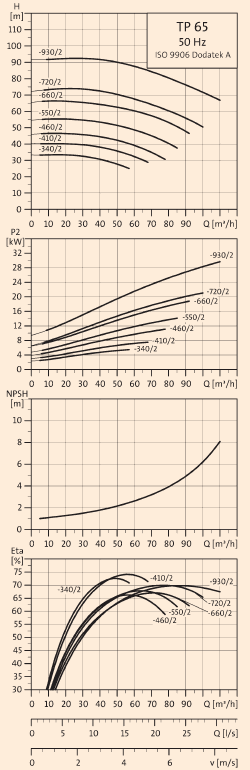 Obr. 2 - Charakteristiky oběhového čerpadla |
Δpe = Δper . (ρr / ρ)2, (12)
kde Δpe je pokles tlakové energie v sací části čerpadla při referenční teplotě vody (kPa).
Příklad
Zadání
Pro oběhové čerpadlo, jehož charakteristiky jsou na diagramech (obr. 2), má být určen minimální i provozní statický přetlak v sacím hrdle čerpadla. Oběhové čerpadlo má zajistit průtok vody ve výši V = 74 m3 . h-1 o teplotě 120 °C, při barometrickém tlaku pb = 98 kPa.
Řešení
Nejprve z tab. 1 odečteme hustoty vody. Při teplotě 20 °C je hustota vody ρr = 998,2 kg . m-3, při teplotě 120 °C je hustota ρ = 943,4 kg . m-3. Dále odečteme tlaky vodní páry na mezi sytosti. Při teplotě 20 °C je ppr = 2,34 kPa, při 120 °C je pp = 198,5 kPa.
Podle (10) bude referenční průtok
Vr = V . ρ / ρr, = 74 . 943,4 / 998,2 = 70 m3 . h-1.
Pro referenční průtok lze v diagramech (obr. 2) odečíst hodnotu NPSH = 3,2 m a také rychlost vody v sacím hrdle v1r = 5,5 m . s-1 (vše při referenční teplotě vody 20 °C).
Podle (11) bude skutečná rychlost vody
v1 = v1r . ρr / ρ, = 5,5 . 998,2 / 943,4 = 5,8 m . s-1.
Podle (6) bude dynamický tlak v sacím hrdle OČ
pd1 = 5 . 10-4 . v12 . ρ = 5 . 10-4. 5,82 . 943,4 = 15,9 kPa.
Podle (9) bude referenční pokles tlakové energie v sací části čerpadla
Δper = 10-3 . ρr . g . NPHS = 10-3 . 998,2 . 9,81 . 3,2 = 31,3 kPa.
Podle (12) bude skutečný pokles tlakové energie v sací části čerpadla
Δpe = Δper . (ρr / ρ)2 = 31,3 . (998,2 / 943,4)2 = 35,1 kPa.
Minimální statický přetlak v sacím hrdle čerpadla potom bude podle vztahu (5)
ps1m = pp + Δpe - pb - pd1 = 198,5 + 35,1 - 98 - 15,9 = 119,7 kPa.
Provozní statický přetlak v sacím hrdle čerpadla bude dán vyšší z hodnot
ps1 = ps1m + 5 = 119,7 + 5 = 124,7 kPa,
ps1 = ps1m + 0,15 . Δpe = 119,7 + 0,15 . 35,1 = 125 kPa.
Poznámka
Pokud by čerpadlem proudila voda o referenční teplotě 20 °C, byla by hodnota minimálního statického přetlaku v sacím hrdle čerpadla
ps1m = 2,34 + 31,3 - 98 - 15,1 = -79,5 kPa,
takže v sacím hrdle čerpadla bude pro studenou vodu postačovat i podtlak (tlak je 98 - 79,5 = 18,5 kPa).
Stanovení hodnoty 15,1 kPa pro referenční dynamický tlak v sacím hrdle OČ ponechávám na čtenáři.
Použitá literatura
Bláha, J. Brada, K.: Příručka čerpací techniky. Vydavatelství ČVUT, Praha 1997.
Klepš, Z. Nožička, J. a kol.: Technické tabulky. SNTL, Praha 1977.
Firemní podklady Grundfos. Olomouc 2004.