Anizotropný model slnečného žiarenia pre potreby dynamických simulácií budov
Z hľadiska tepelných simulácií budov je jednou z najvýznamnejších okrajových podmienok tepelný výkon privádzaný na jednotlivé povrchy konštrukcie slnečným žiarením. Keďže hodnoty intenzity slnečného žiarenia bývajú meteorologickými stanicami merané spravidla na horizontálnom povrchu, je potrebné tieto prepočítať. Príspevok sa zaoberá prepočtom celkovej intenzity slnečného žiarenia na horizontálnom povrchu na intenzitu slnečného žiarenia obecne orientovaného vertikálneho povrchu a uvádza simulované priebehy jednotlivých parametrov v rozsahu devätnástich dní.
1. Teoretický úvod
Rozmach informačných technológií v posledných niekoľkých desaťročiach umožnil vývoj pokročilých riadiacich algoritmov, využívajúcich predpovede počasia a termodynamické modely riadeného objektu. To umožňuje predikovať vývoj vnútorných teplôt v krátkodobom časovom horizonte a nastaviť parametre regulácie tak, aby sa minimalizovala spotreba energie a zároveň boli splnené požadované kritéria tepelného komfortu.
Úspešnosť nasadenia regulácie závisí predovšetkým od kvality použitého predikčného modelu, ktorý musí byť schopný s dostatočnou presnosťou zachytiť dynamiku procesu a vhodne zvoleného predikčného horizontu.
Predikčný model predstavuje náhradný dynamický model umožňujúci simulácie správania sa reálneho systému. Pri procese modelovania sa obvykle zachovávajú len zložky, vlastnosti alebo vzťahy systému, ktoré sú pre daný účel opodstatnené. Každý takýto model je opísateľný sústavou obyčajných, respektíve parciálnych diferenciálnych rovníc, ktorých riešenie popisuje proces v priestore a čase, v závislosti na geometrickom tvare telesa, jeho fyzikálnych vlastnostiach a zadaných okrajových či počiatočných podmienkach.
V prípade tepelných simulácií budov je jednou z najvýznamnejších okrajových podmienok tepelný výkon privedený na jednotlivé povrchy konštrukcie slnečným ožiarením. Keďže väčšina meteorologických meracích staníc uvádza len hodnoty celkového slnečného ožiarenia na horizontálnej rovine, je nutné získané dáta ďalej upraviť s uvážením sklonu a orientácie modelovaného povrchu. Pre bežné inžinierske výpočty bývajú postačujúce izotropické modely. Z pohľadu presnosti dynamických simulácií je obvykle nevyhnutné použiť anizotropický model oblohy, ktorý zohľadňuje nárast difúzneho žiarenia v blízkosti slnečného kotúča a horizontu.
Príspevok sa zaoberá prepočtom celkového slnečného ožiarenia na horizontálnom povrchu na slnečné ožiarenie obecne nakloneného a orientovaného povrchu s využitím anizotropického modelu. Takto upravené dáta je neskôr možné využiť k simulácii tepelného výkonu privádzaného na jednotlivé povrchy stavebnej konštrukcie.
Obr. 1 Zložky slnečného ožiarenia dopadajúce na zemský povrch
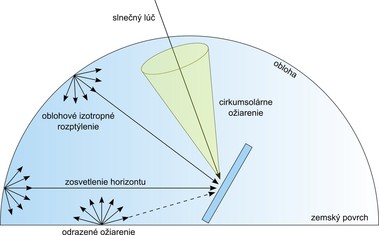
Celkové slnečné ožiarenie dopadajúce na zemský povrch možno rozdeliť na priamu a difúznu zložku. Na rozdiel od priameho ožiarenia, ktoré dopadá na povrch pod uhlom určeným okamžitou polohou Slnka, je difúzna zložka viac či menej rovnomerne rozptýlená prechodom cez atmosféru.
Z hľadiska uvažovaného mechanizmu dopadu sa difúzna zložka ďalej rozdeľuje na cirkumsolárne ožiarenie, oblohové izotropné rozptýlenie a zosvetlenie horizontu. Predpokladá sa, že cirkumsolárne difúzne ožiarenie dopadá na zemský povrch z rovnakého smeru ako priame slnečné ožiarenie, s tým rozdielom, že v dôsledku rozptylu v atmosfére je smerované v podstatne väčšom priestorovom uhle. Oblohové izotropné rozptýlenie je na rozdiel od cirkumsolárnej zložky atmosférou rozptýlené v takej miere, že sa vo všetkých smeroch uvažuje rovnako intenzívne. Zosvetlenie od horizontu je prírastok difúzneho ožiarenia spôsobený nárastom plochy, na ktorú dopadá žiarenie prechádzajúce atmosférou v blízkosti horizontu.
2. Model slnečného ožiarenia
2.1 Výpočet mimozemského slnečného ožiarenia na vodorovnej rovine
Pod pojmom mimozemské slnečné ožiarenie je myslené celkové žiarenie, ktoré by sa mohlo dosiahnuť v prípade, že by na Zemi neexistovala atmosféra [1]. Výpočet mimozemského slnečného ožiarenia je dôležitý pri určovaní priamej a difúznej zložky z nameraných dát na horizontálnej rovine a možno ho určiť podľa vzťahu
(1)
Uhol zenitu, definovaný ako uhol medzi vertikálou a spojnicou so slnkom sa potom určí ako
(2)
kde je
- G
- – slnečná konštanta [W/m2]
- n
- – poradie dňa v roku [–]
- ϕ
- – zemepisná šírka [°]
- δ
- – slnečná deklinácia [°]
- ω
- – hodinový uhol [°]
Veľkosť mimozemského ožiarenia je charakterizovaná slnečnou konštantou, ktorá vyjadruje slnečné ožiarenie dopadajúce na plochu jedného štvorcového metra kolmo na os slnečného lúča za jednotku času meranú mimo zemskej atmosféry. Jej hodnota je závislá od vzájomnej vzdialenosti Zeme a Slnka. Organizácia The World Radiation Center [2] definuje strednú hodnotu slnečnej konštanty ako 1367 W/m2 (v strednej vzdialenosti Zeme od Slnka v priebehu roku).
Jedným z najdôležitejších parametrov z rovnice (2), potrebným pre výpočet výšky Slnka nad horizontom je slnečná deklinácia [3]. Táto vyjadruje uhol zovretia medzi spojnicou stredu Slnka so stredom Zeme s rovinou zemského rovníku. Pri rotácii Zeme okolo Slnka dochádza v priebehu roka k periodickým zmenám v slnečnej deklinácii, s ohľadom na zanedbateľnú chybu sa ale pre potreby technických výpočtov uvažuje jej hodnota v priebehu dňa konštantná [4]. Pre ľubovoľný deň v roku sa hodnota slnečnej deklinácie určí ako
(3)
kde parameter B zohľadňujúci poradie dňa v roku sa vypočíta ako
(4)
Čas v rovnici (2) je vyjadrený hodinovým uhlom, ktorý vyjadruje zdanlivý pohyb Slnka nad poludníkmi. Pretože rýchlosť rotácie Zeme je približne 15° za hodinu, vypočíta sa hodinový uhol nasledovne [5]
(5)
pričom slnečný čas sa určí zo vzťahu
(6)
kde je
- Lst
- – poloha štandardného poludníka [°]
- Loc
- – poloha lokálneho poludníka [°]
Parameter E v rovnici (6) reprezentuje časovú korekciu v minútach
(7)
2.2 Index čistoty atmosféry
V prípade, že sú k dispozícii namerané hodnoty celkového slnečného ožiarenia na horizontálnej rovine je možné stanoviť, aké percento mimozemského ožiarenia dopadá na zemský povrch pomocou indexu čistoty atmosféry nasledovne
(8)
kde je
- I
- – celkové slnečné ožiarenie merané pyranometrom na horizontálnej rovine [W/m2]
Na základe vypočítanej hodnoty kT možno celkové slnečné ožiarenie rozdeliť na priamu a difúznu zložku. Podľa Erbs a kol. [6] sa difúzna zložka slnečného ožiarenia určí nasledovne
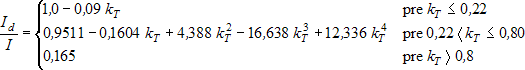(9)
kde je
- Id
- – difúzna zložka slnečného ožiarenia na vodorovnej rovine [W/m2]
Pre priamu zložku slnečného ožiarenia na horizonte následne platí
2.3 Výpočet celkového slnečného ožiarenia na naklonenom povrchu
Pre potreby tepelných simulácií budov je výpočet slnečného ožiarenia na horizontálnom povrchu nepostačujúci, z dôvodu rôznej orientácie plôch voči dopadajúcemu slnečnému žiareniu. Ďalej je preto nutné stanoviť celkové množstvo slnečného ožiarenia dopadajúceho na obecný povrch oslnenej steny podľa rovnice
(11)
Tento vzťah je výsledkom práce viacerých autorov a vyjadruje celkové slnečné ožiarenie dopadajúce na sklonený povrch ako súčet priamej, difúznej a odrazenej zložky so zahrnutím anizotropie oblohy. Priame slnečné ožiarenie dopadajúce na naklonený povrch je korigované pomocou geometrického faktora, ktorý je pomerom ožiarenia dopadajúceho na naklonený povrch ku ožiareniu na horizontálnom povrchu v rovnakom čase [2], teda platí
(12)
V prípade, že sa menovateľ rovnice blíži k nule, rovnica nedáva uspokojivé výsledky. Z toho dôvodu je nutné pre povrchy oslnené v čase východu a západu Slnka získať hodnoty geometrického faktoru integráciou rovnice (12) v intervale ω1 až ω2 nasledovne
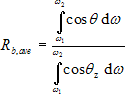(13)
pričom kosínus uhlu dopadu ožiarenia θ sa pre vertikálnu stenu vypočíta ako
(14)
kde je
- γ
- – azimut povrchu [°]
Priama zložka slnečného ožiarenia dopadajúceho na naklonenú rovinu sa vypočíta ako
Stanovenie zložiek difúzneho ožiarenia je pomerne komplexná problematika. Hottel a Woertz [7] vytvorili model oblohového izotropického rozptýlenia, za predpokladu rovnomerného rozloženia difúzneho slnečného ožiarenia dopadajúceho z oblohy. V takomto prípade platí, že difúzne ožiarenie závisí len od hodnoty uhlového faktoru. Pre povrch sklonený od horizontálnej roviny o uhol β potom platí
(15)
V prípade zatiahnutej oblohy je model veľmi dobrou aproximáciou, avšak pri dominantnom priamom ožiarení dochádza k zhoršovaniu presnosti, spôsobenom prítomnosťou anizotropickej zložky v dôsledku narastajúcej intenzity difúzneho ožiarenia v blízkosti Slnka alebo horizontu. Hay a Davies [8] doplnili izotropický model o cirkumsolárnu zložku difúzneho ožiarenia. Uvažujúc jasnú oblohu, cirkumsolárna zložka spolu s oblohovým izotropickým rozptýlením majú anizotropický charakter, teda pre anizotropický index platí
(16)
Tento vyjadruje pomer difúzneho ožiarenia považovaného z väčšej časti za cirkumsolárne, pričom zostávajúca časť sa predpokladá izotropická. Pri jasnej oblohe je hodnota anizotropického indexu vysoká, s prevládajúcou cirkumsolárnou zložkou. Naproti tomu, pri zatiahnutej oblohe sa hodnota anizotropického indexu blíži k nule a v modeli sa uvažuje len s oblohovým izotropickým rozptýlením. Pre cirkumsolárnu zložku na naklonenom povrchu teda platí
Keďže cirkumsolárne slnečné ožiarenie pochádza z oblasti blízkej okoliu Slnka, počíta sa obdobným spôsobom ako priame slnečné ožiarenie. Zostávajúca izotropická difúzna časť sa potom stanoví ako
(18)
Spojením rovníc (17) a (18) dostávame vzťah pre úplný Hay-Daviesov model difúznej zložky slnečného ožiarenia v tvare
(19)
Reindl [9] na základe práce Klutchera [10] rozšíril difúzny model (19) o zosvetlenie horizontu, čím dostávame celkové difúzne ožiarenie na naklonenom povrchu v tvare
(20)
kde modulačný faktor f sa určí ako
(21)
| Odrážajúci povrch | ρg |
|---|---|
| Dokonalé čierne teleso | 0,00 |
| Zelená tráva | 0,26 |
| Kremenný piesok | 0,35 |
| Betón | 0,40 |
| Červená tehla | 0,44 |
| Čerstvý sneh | 0,85 |
| Ideálny biely povrch | 1,00 |
Poslednou zložkou slnečného ožiarenia, ktorú je nutné uvažovať v simulačnom modeli je ožiarenie odrazené od povrchu zeme. Množstvo pohltenej a odrazenej energie je ovplyvňované optickými vlastnosťami povrchu. Pre výpočet odrazenej zložky je potrebné odhadnúť parameter odrazivosti, ktorý vyjadruje pomer odrazeného slnečného k celkovému dopadajúcemu ožiareniu. Hodnoty odrazivosti sa pohybujú v rozmedzí od nula do jedna, v závislosti od druhu pokrytia povrchu, ako uvádza Tab. 1.
Liu a Jordan [12] odporúčajú hodnoty odrazivosti horizontálnych povrchov 0,2 pre objekty nachádzajúce sa v mestách bez snehovej pokrývky a 0,7 so snehovou pokrývkou. Pre slnečné ožiarenie odrazené od povrchu zeme potom platí
(22)
3. Simulácia slnečného ožiarenia
Na základe postupu uvedeného v teoretickej časti bol v programovom prostredí MATLAB vytvorený anizotropický model oblohy, platný pre ľubovoľný sklon a orientáciu ožiarenej plochy. Za účelom simulácie tepelného výkonu privedeného do budovy bol model aplikovaný na obvodovú stenu školskej učebne A2/312 Fakulty strojního inženýrství, Vysokého učení technického v Brně. Azimut povrchu odpovedá uhlu 135°. Aby bolo možné zachytiť dynamický charakter slnečného žiarenia s dostatočnou presnosťou, bol použitý časový krok 6 minút. Neuvažuje sa zo zatienením od okolitých objektov areálu školy.
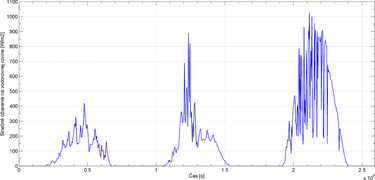
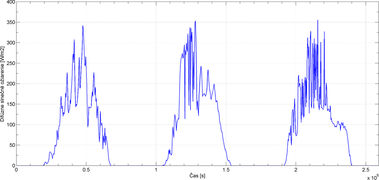
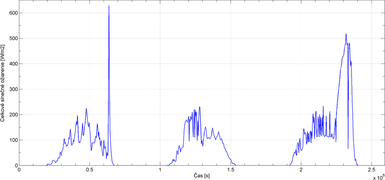
Hodnoty slnečného ožiarenia na vodorovnej rovine sú získané zo záznamu permanentnej družicovej stanice TUBO [13] pre oblasť Brna (49° 12' 21" s. š., 16° 35' 34" v. d.) v období od 25. 8. 2012 do 12. 9. 2012. Priebehy slnečného ožiarenia v rozsahu prvých troch dní sú pre ilustráciu znázornené na Obr. 2, 3, 4, 5 a 6.
Obr. 2 Celkové slnečné ožiarenie na vodorovnej rovine
Obr. 3 Index čistoty atmosféry
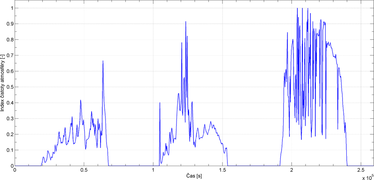
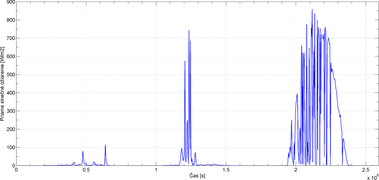
Z priebehu celkového slnečného ožiarenia na vodorovnej rovine (Obr. 2) a indexu čistoty atmosféry (Obr. 3) je možné prerozdeliť hodnoty priamej a difúznej zložky na vodorovnej rovine (Obr. 4, 5).
Obr. 4 Priama zložka slnečného ožiarenia na vodorovnej rovine
Obr. 5 Difúzna zložka slnečného ožiarenia na vodorovnej rovine
Obr. 6 Celkové slnečné ožiarenie na zvislej ploche s azimutom 135°
Pomocou rovnice (11) sa potom stanoví celkové množstvo slnečného ožiarenia dopadajúce na obvodovú stenu (Obr. 6).
4. Vyhodnotenie výsledkov
Za účelom vyhodnotenia simulovaných priebehov slnečného ožiarenia boli pre jednotlivé uvažované dni vypočítané denné dávky slnečného ožiarenia. Tieto sa stanovia integráciou okamžitého slnečného ožiarenia plochy v intervale teoreticky možnej doby slnečného svitu nasledovne
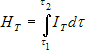(23)
kde je
- IT
- – okamžité slnečné ožiarenie plochy [W/m2]
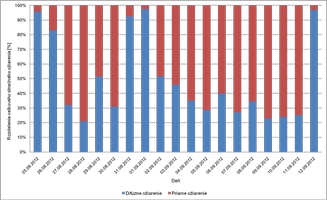
Uvedeným spôsobom boli z priebehov slnečného ožiarenia vypočítané denné dávky slnečnej energie. Percentuálny podiel priameho a difúzneho slnečného ožiarenia na vodorovnej rovine v sledovanom období je znázornený v Obr. 7.
Obr. 8 ukazuje porovnanie dennej dávky celkového slnečného ožiarenia na vodorovnej rovine a zvislej ploche s azimutom 135°. Z obrázku je zrejmé, že vzhľadom k severozápadnej orientácii dopadá na povrch obvodovej steny pomerne malá časť celkového slnečného ožiarenia.
Obr. 7 Rozdelenie celkového slnečného ožiarenia na vodorovnej rovine
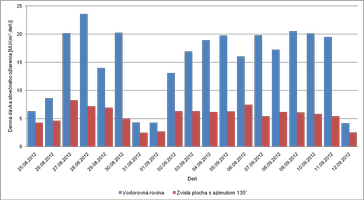
Obr. 8 Porovnanie dennej dávky slnečného ožiarenia na vodorovnej rovine a zvislej ploche s azimutom 135°
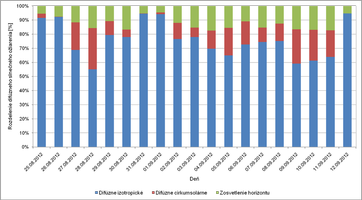
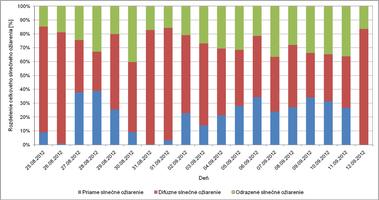
Obr. 9 znázorňuje rozdelenie jednotlivých zložiek slnečného ožiarenia na povrchu obvodovej steny školskej učebne. V dňoch, kedy prevláda jasná obloha je vplyv anizotropie pomerne vysoký, čo dokazuje aj podiel cirkumsolárnej difúznej zložky a zosvetlenia horizontu na celkovom slnečnom ožiarení plochy. V opačnom prípade prevláda v modeli izotropické difúzne rozptýlenie.
Obr. 10 ukazuje percentuálny podiel jednotlivých zložiek slnečného ožiarenia na obvodovej stene školskej učebne. Z porovnania vidieť, že odrazená zložka slnečného ožiarenia tvorí v prípade zvislo orientovaných plôch nezanedbateľnú súčasť celkového slnečného ožiarenia.
Obr. 9 Rozdelenie difúzneho slnečného ožiarenia na zvislej plochy s azimutom 135°
Obr. 10 Rozdelenie celkového slnečného ožiarenia na zvislej ploche s azimutom 135°
5. Záver
Uvedený postup sa využíva v tepelných simuláciách budov. Prepočítaním celkového slnečného ožiarenia meraného na vodorovnej rovine na slnečné ožiarenie ľubovoľne orientovanej plochy je možné v tepelnom modeli budovy simulovať tepelný výkon privedený na vonkajší povrch konštrukcie slnečným ožiarením. V prípade, že oslnená stena obsahuje transparentné plochy, je potrebné ďalej vypočítať slnečné ožiarenie prenikajúce zasklením a jeho následnú distribúciu na jednotlivé vnútorné plochy.
Poďakovanie
Článok bol spracovaný s finančnou podporou projektu FSI-S-11-6 s názvom „Komplexní modelování interakce člověka a prostředí v kabinách dopravních prostředků a obytných prostorách a návrhové nástroje“.
Použitá literatúra
- [1] TIWARI, G. N. Solar energy: fundamentals, design, modelling, and applications. 3. print. Pangbourne, England: Alpha Science International Ltd, 2002. ISBN 978–084–9324–093.
- [2] DUFFIE, John A.; William A. BECKMAN. Solar Engineering of Thermal Processes. 3rd edition. Hoboken: John Wiley, 2006, xix, 908 s. ISBN 978–0–471–69867–8.
- [3] ČSN 73 4301. Obytné budovy. Praha: Český normalizační institut, 2004.
- [4] KAŇKA, J. Deklinace slunce v průběhu desetiletí. [online]. [cit. 2013-05-28]. Dostupné z:
http://stavba.tzb-info.cz/denni-osvetleni-a-osluneni/8381-deklinace-slunce-v-prubehu-desetileti - [5] MASTERS, Gilbert M. Renewable and efficient electric power systems. Hoboken, NJ: John Wiley, 2004, xx, 654 p. ISBN 04-712-8060-7.
- [6] EICKER, U. Solar technologies for buildings. Chichester: Wiley, c2003, xii, 323 s. ISBN 978-0-471-48637-4.
- [7] HOTTEL, H. C; WOERTZ, B. B. Performance of flat-plate solar heat collectors. Transactions of American Society of Mechanical Engineers. 1942, 64, s. 91.
- [8] HAY, J. E; DAVIES, J. A. Calculation of the solar radiation incident on an inclined surface. Proceedings First Canadian Solar Radiation Data Workshop. 1980, s. 59–72.
- [9] REINDL, D. T. Estimating diffuse radiation on horizontal surfaces and total radiation on tilted surfaces. Madison, 1988, xiv, 208 s. Diplomová práca. University of Wisconsin-Madison.
- [10] KLUCHER, T. M. Evaluation of models to predict insolation on tilted surfaces. Solar Energy. 1979, 23, s. 111–114.
- [11] RADOSAVLJEVIĆ, J.; DORDEVIĆ, A. Defining of the intensity of solar radiation on horizontal and oblique surfaces on earth. Working and Living Environmental Protection. 2001, vol. 2, s. 77–86.
- [12] LIU, B. Y. H.; JORDAN, R. C. The long term average performance of flat-plate solar energy collectors. Solar Energy. 1977, 19, s. 87–89.
- [13] TUBO, Permanentní GPS stanice. [online].[cit. 2013-04-30]. Dostupné z: http://tubo.fce.vutbr.cz/new
One of the most important boundary conditions occuring in the thermal building simulations is the thermal power penetrated into building elements as a result of the solar radiation. Intensities of the solar radiation are usually measured by weather-stations on the horizontal plane, and thus not directly applicable for the computations. Paper provides the methodology for recomputation of the total solar radiation measured by the pyranometer on the horizontal surface to the intensities of arbitrarily oriented wall and provides simulation results for the nineteen days.
