Regulační armatury - teoretická základna (II)
Teoretická základna je seriál článků se zaměřením na teorii základních regulačních prvků. Je určen především odborné veřejnosti, studentům, projektantům nebo provozovatelům tepelných soustav. Cílem je dostupnost teoretických informací s uvedením příkladů návrhu regulačních prvků do otopných soustav. Tento díl je zaměřen na teorii s uvedením základních výpočtových vztahů a příkladu návrhu regulačního ventilu.
Charakteristiky ventilů
Statickou charakteristikou ventilu rozumíme závislost poměrného průtoku resp. kv hodnoty vztažené ke kvs hodnotě na poměrném zdvihu ventilu. Hlavní dvě charakteristiky jsou lineární a rovnoprocentní.
Nejnižší kv hodnota, při které má charakteristika ještě normální sklon, se označuje jako kvR hodnota (obr. 5). Poměr
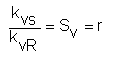
se označuje jako akční poměr, resp. regulační rozsah. Pod kvR hodnotou se stává regulace nestabilní. Proto je třeba navrhovat ventil tak, aby se jeho pracovní oblast pohybovala vždy nad kvR hodnotou.
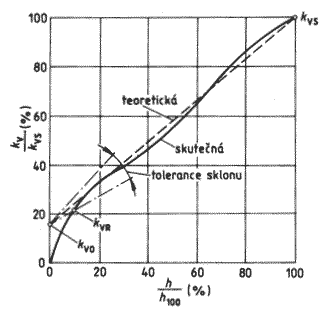
Obr. 5 - Lineární statická charakteristika ventilu
Obvyklé hodnoty regulačního rozsahu jsou 20 až 30 a u těch nejlepších ventilů až 50. Čím je akční poměr, resp. regulační rozsah větší, tím k lepší regulaci dochází při nízkých výkonech.
Skutečné charakteristiky mají v blízkosti nulového zdvihu odlišný průběh od teoretických charakteristik, tj. proložených (obr. 5 a 6). Měli bychom se tedy vyvarovat toho, aby ventily pracovaly v oblasti zdvihu do 10 %.
Rovněž důležitou hodnotou vzhledem k definování charakteristik ventilů je poměrný průtokový součinitel Φ, který je definován poměrem
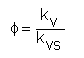
a poměrný průtokový součinitel při nulovém zdvihu ![]() 0, který je dán průsečíkem proložené charakteristiky s osou y (viz obr. 5-5) a který je tak definován poměrem
0, který je dán průsečíkem proložené charakteristiky s osou y (viz obr. 5-5) a který je tak definován poměrem
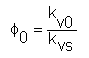
U lineární statické charakteristiky ventilu odpovídá stejné změně zdvihu h stejná změna kv hodnoty. U lineární charakteristiky tak dojde při zvětšení zdvihu o 1 % ke zvýšení poměrného průtoku přibližně též o 1 %. Této skutečnosti odpovídá vztah
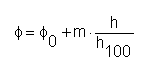
kde m udává sklon charakteristiky.
U rovnoprocentních charakteristik odpovídá stejné změně zdvihu h procentuálně stejná změna kv hodnoty. To znamená, že charakteristika má tvar, který definuje vztah
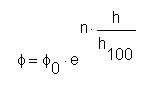
Vynášíme-li rovnoprocentní charakteristiku v logaritmické stupnici, zjistíme sklon křivky jako
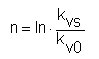
což je exponent ve výše uvedené rovnici.

Obr. 6 - Příklad lineární a rovnoprocentní statické charakteristiky s ![]() 0 = 4 %
0 = 4 %
LIN - lineární statická charakteristika teoretická
SLIN - lineární statická charakteristika skutečná
RP - rovnoprocentní statická charakteristika teoretická
Pro dosažení regulačního rozsahu 50 je potřebné použít minimálně tzv. čtyřprocentní charakteristiku. U takovéto charakteristiky podle obr. 7 při zvětšení zdvihu o 1 % pro ventil s kvs = 100 a kv0 = 4 dojde ke zvýšení o 4,13 %.
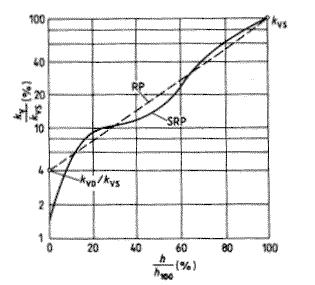
Obr. 7 - Příklad rovnoprocentní statické charakteristiky s ![]() 0 = 4 % v logaritmické stupnici
0 = 4 % v logaritmické stupnici
RP - rovnoprocentní statická charakteristika teoretická
SRP - rovnoprocentní statická charakteristika skutečná
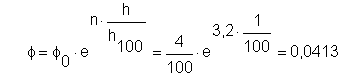
Z výše uvedeného vyplývá jedno doporučení. Ve spodní teplotní oblasti (přechodné období, požadované malé výkony) a při nižší autoritě ventilu je pro regulaci lepší použít rovnoprocentní ventil s velkým regulačním rozsahem. V komplikovaných případech lze regulaci rozložit na dva ventily za sebou.
Teoreticky je možné zvolit jakoukoli jinou statickou charakteristiku než jsou dvě dříve uvedené. Nová charakteristika tak může lépe vyhovět konkrétní aplikaci. Většinou jde o tzv. modifikované rovnoprocentní charakteristiky.
Změna výkonu
Použijeme-li např. u výměníku či otopného tělesa regulačního ventilu, vyjádří změnu výkonu funkční závislost
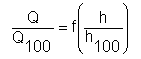
kde:
Q tepelný výkon otopného tělesa [W]
Q100 jmenovitý tepelný výkon otopného tělesa [W]
h zdvih kuželky ventilu [mm]
h100 maximální zdvih kuželky ventilu [mm]
Závislost tepelného výkonu na zdvihu ventilu bude dále vyjádřena jako charakteristika výměníku s ventilem. Změna průtoku ventilem v závislosti na zdvihu je prostředkem k dosažení potřebné změny tepelného výkonu (obr. 8).
Závislost
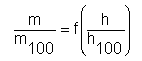
kde:
m hmotnostní průtok [kg/s]
m100 hmotnostní průtok při maximálním zdvihu [kg/s]
lze označit jako průtočnou charakteristiku ventilu. Prostřednictvím průtočné charakteristiky lze popsat chování výměníku s ventilem, pokud je známa závislost
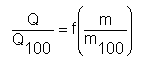
tedy výkonová charakteristika. Regulační postup, při kterém se dosáhne změny tepelného výkonu změnou průtoku, lze označit jako regulaci škrcením, tedy regulaci množství - kvantitativní.
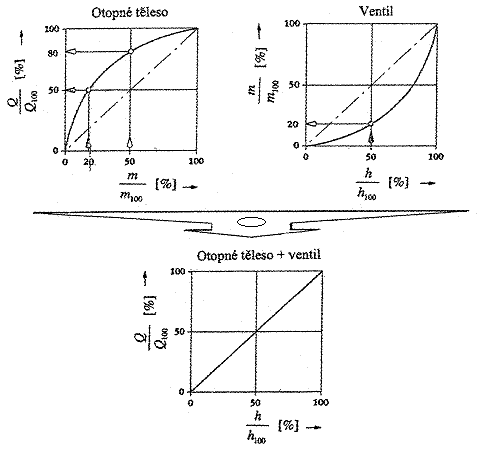
Obr. 8 - Spojením charakteristiky otopného tělesa (obecně výměníku tepla)
a ventilu získáme výkonovou charakteristiku otopného tělesa s ventilem
Příklad
Pro regulaci potrubní sítě na obr. 9 navrhněme regulační ventil. Tlaková ztráta sítě Δps = 20 kPa. Potrubní síť je z potrubí DN 65. Přenášený tepelný výkon Q = 250 kW při teplotním rozdílu 20 K a střední teplotě vody 80 °C.
Jako minimální autoritu ventilu volme hodnotu Pv = 0,33 a poměrná autorita tak bude Pv/ = 0,5. Požadovaná tlaková ztráta ventilu je
![]()
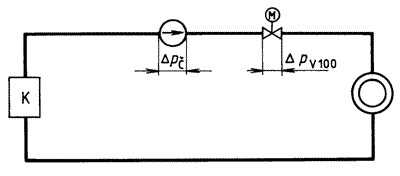
Obr. 9 - Schéma okruhu pro příklad
Abychom mohli navrhnou správný ventil, musíme určit jeho kvs hodnotu. Průtok ventilem je
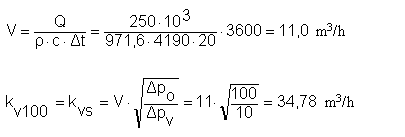
V tabulce 1 máme dvě provedení ventilu: X, kterému přísluší provedení se zmenšeným průtočným průřezem sedla, a Y, jehož průtočný průřez odpovídá přibližně DN 65. Ventilu DN 65 by tak odpovídaly hodnoty kvs = 38 a 60 m3/h, ale vypočtené hodnotě kvs = 34,78 m3/h pak ventily DN 65X a DN 50Y. Ventil DN 50Y bude sice o něco levnější, avšak vyžaduje vícepráce na redukci potrubí.
| DN | 15 | 20 | 25 | 32 | 40 | 50 | 65 |
| Provedení X | 2,4 | 3,8 | 6,0 | 9,6 | 15 | 24 | 38 |
| Provedení Y | 3,8 | 6,0 | 9,6 | 15 | 24 | 38 | 60 |
| Tab. 1 - kvs hodnoty pro provedení regulačních ventilů X a Y |
Použitá literatura:
Hydraulika a řízení otopných soustav - autor. Ing. Jiří Bašta Ph.D. vydavatelství ČVUT Praha 2003