Regulační armatury - teoretická základna (I)

REGULAČNÍ ARMATURY

Aby regulační ventily plnily správně svou funkci, musejí mít vlastnosti vhodné pro dané použití. Vlastnosti ventilu jsou dány především jeho konstrukcí, tj. průtočným průřezem, tvarem průtočných cest a kuželky, ale rovněž vlastnostmi ovládacího pohonu ventilu.

Při výběru ventilu jsou důležitá následující kritéria:

jmenovitý tlak PN přípustný rozdíl tlaků kv hodnota ventilu charakteristika ventilu autorita ventilu Pv

Příklad nejčastěji používaných tvarů kuželek ventilů je na obr. 1.

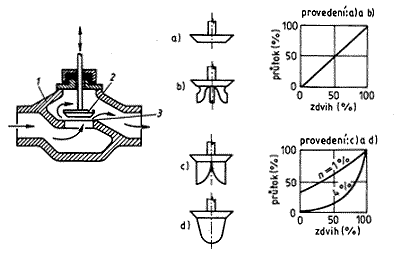Obr. 1: Princip funkce ventilu a nejběžnější tvary kuželek
a) talířová kuželka s kónickými dosedacími plochami b) talířová kuželka s usměrňujícími žebry c) kuželka s logaritmickými vstupy d) kuželka s logaritmickým nátokovým profilem	1 - tělo ventilu, 2 - kuželka ventilu, 3 - sedlo ventilu

1 Charakteristiky a základní veličiny

1.1 Jmenovitý průtok - k_v hodnota

Velikost ventilu je určena k_vs hodnotou. k_vs hodnota vyčísluje vztah mezi nastavením ventilu (zdvih, úhel natočení) a protékajícím množstvím. Představuje tak jmenovitý průtok armaturou v m³/h při maximálním otevření h₁₀₀ armatury a tlakové ztrátě Δp_o = 100 kPa = 1 bar. Pro vodu jako teplonosnou látku počítáme se zjednodušeným vztahem:

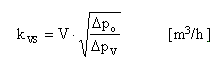
kde:
V          je objemový průtok armaturou [m³/h] !
Δp_V      tlaková ztráta ventilu [kPa]
Δp_o = 100 kPa (= 1 bar)

Z takto zapsaného základního vztahu můžeme určit ze známé k_vs hodnoty a pro požadovaný průtok tlakovou ztrátu ventilu, či z požadované tlakové ztráty na ventilu a požadovaného průtoku ventilem k_vs hodnotu a podle ní vybrat příslušný ventil, nebo ze známé k_vs hodnoty ventilu a tlakové ztráty na ventilu určit skutečný průtok ventilem.

Pro výpočet k_vs hodnoty při jiné teplonosné látce než je voda se používá následující vztah:

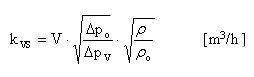
kde:
ρ     hustota teplonosné látky při provozní teplotě [kg/m³]
ρ_o    hustota vody při teplotě 15 °C [kg/m³]

V USA se počítá s C_vs hodnotou, která je zjišťována stejným způsobem při tlakové ztrátě na ventilu 1 psi (Δp_o = 1 lb/sq = 6,8948 kPa) a průtok je v gal/min. Hustota je dosazována v lb/ft³ (1 lb/ft³ = 16,018 kg/m³).

Dříve se u nás jako ekvivalent ke k_vs hodnotě používal průtokový součinitel A_vs, který jednoznačně určuje vlastnosti armatury, ale je do něj dosazováno důsledně v základních jednotkách SI. Průtokový součinitel je definován jako:

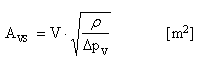
kde:
V      je objemový průtok ventilem [m³/s]
Δp_V    tlaková ztráta ventilu [Pa]
ρ      hustota vody [kg/m³]

Přepočet jednotlivých hodnot vypadá následovně:

kvs = 36000.Avs	[m3/h]
kvs = 0,865.Cvs	[m3/h]
Cvs = 41700.Avs	[gal/min]
Cvs = 1,17.kvs	[gal/min]
Avs = 2,40.10-5.Cvs	[m2]
Avs = 2,78.10-5.kvs	[m2]

Mezi k_v hodnotou, volným průtočným průřezem připojovacího potrubí ventilu S [mm²] a součinitelem místního odporu ventilu ζ [-] existují následující vztahy:

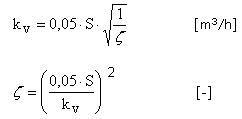
k_v hodnota, kterou dostaneme při maximálním zdvihu kuželky h = 100 %, je označována jako k_vs hodnota. k_v0 označíme k_v hodnotu, kterou získáme extrapolací pro nulovou hodnotu zdvihu kuželky h = 0 % (viz obr. 5 v druhém dílu). Obvyklé k_v hodnoty ventilů se pohybují v rozmezí 0,25 až 500 m³/h.

Autorita ventilu P_v

Podstatný vliv na regulační schopnost ventilu umístěného v potrubní síti má autorita ventilu. Obecně lze konstatovat, že čím je větší autorita ventilu, tím lepší je regulační schopnost ventilu v potrubní síti.

Autorita ventilu P_v (dříve označována a) je definována poměrem tlakové ztráty ventilu při plném otevření ku tlakové ztrátě ventilu při plném uzavření.

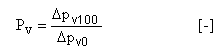
kde:
p_v100     tlaková ztráta ventilu při plném otevření [Pa]
p_v0        tlaková ztráta ventilu při plném uzavření [Pa]
P_v         autorita ventilu [-]

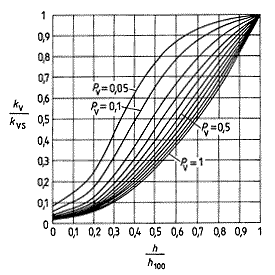
Podle toho, jakou má ventil tlakovou ztrátu vzhledem k tlakové ztrátě potrubní sítě okruhu příslušejícího ventilu, resp. jak veliká je autorita ventilu, se statická charakteristika ventilu deformuje. Deformaci statické charakteristiky ventilu s lineární, rovnoprocentní a parabolickou charakteristikou v závislosti na autoritě ventilu ukazují obr. 2, 3 a 4.

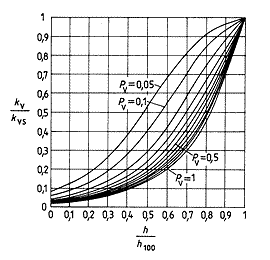Obr. 2 - Deformace rovnoprocentní statické charakteristiky ventilu se změnou autority ventilu

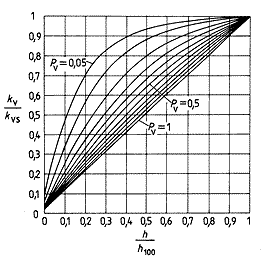Obr. 3 - Deformace lineární statické charakteristiky ventilu se změnou autority ventilu

K určení k_vs hodnoty je zapotřebí jmenovitého průtoku a tlakové ztráty ventilu. Tlakovou ztrátu ventilu při plném otevření lze určit přes autoritu ventilu vztahem:

Nevýhodou tohoto vztahu je, že tlaková ztráta ventilu je sama závislá na tlakové ztrátě ventilu při plném otevření. Předložený vztah je pro praxi neužitečný, a proto se do vztahu promítá tlaková ztráta potrubní sítě okruhu příslušejícího ventilu. Vztah nabývá tvaru:

Obr. 4 - Deformace parabolické statické charakteristiky ventilu se změnou autority ventilu

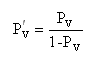
kde:
Δp_PS    tlaková ztráta potrubní sítě okruhu příslušejícího ventilu [Pa]
P_v´       poměrná autorita ventilu [-]

Při obvyklé autoritě ventilu P_v = 0,33 je poměrná autorita P_v´ = 0,5. Tlaková ztráta plně otevřeného ventilu je tak přibližně poloviční, jako tlaková ztráta úseku potrubní sítě bez ventilu. Tlaková ztráta např. výměníku, otopného tělesa či úseku potrubní sítě je známa z technického řešení otopné soustavy.

Regulovatelnost u lineární charakteristiky ventilu je tím příznivější, čím větší je autorita ventilu, neboť s přibývající autoritou ventilu se blížíme k žádanému lineárnímu průběhu statické charakteristiky. Zvýšení autority ventilu znamená, při daných dimenzích potrubní sítě, zvýšení odporu a snížení k_vs hodnoty. Se zmenšující se k_vs hodnotou stoupá tlaková ztráta ventilu, jak ukazuje následující vztah:

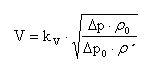
kde:
k_v    jmenovitý průtok [m³/h]
V     objemový průtok [m³/h]
p     tlaková ztráta ventilu [kPa]
p_o    = 100 kPa
ρ     hustota vody při provozní teplotě [kg/m³]
ρ_o    hustota vody při teplotě 15 °C [kg/m³]

Tato zvýšená tlaková ztráta musí být kryta zvýšením dopravního tlaku čerpadla. Z toho plyne, že s rostoucí autoritou ventilu se sice zlepší regulovatelnost zařízení, ale zvyšuje se spotřeba energie čerpadla. Jako směrná hodnota a jakýsi kompromis platí rozmezí autority ventilu P_v = 0,3 až 0,5. S tímto rozmezím se však nedá dosáhnout žádaného lineárního průběhu výsledné charakteristiky při statické lineární charakteristice.

Pro ventily s rovnoprocentní charakteristikou platí však něco jiného. Zde můžeme dosáhnout lineárního průběhu statické charakteristiky dokonce s relativně malou autoritou ventilu. Směrná hodnota P_v = 0,3 až 0,5 zde není žádným kompromisem, jak tomu je u ventilu s lineární charakteristikou.

Pro každé dimenzování lze znázornit a najít optimální autoritu ventilu, která povede k lineární výsledné charakteristice. Pro běžnou praxi se zdá zde popsaný výklad těžko akceptovatelný. Přesto se výše uvedená směrná hodnota používá.

Použitá literatura:
Hydraulika a řízení otopných soustav - autor: Ing. Jiří Bašta Ph.D., vydavatelství ČVUT Praha 2003