Termografie v tepelné technice, teoretické stanovení součinitele prostupu tepla
Termografie je dnes zcela běžně využívána pro diagnostikování kvality obálky budov. Hlavním cílem je obvykle kontrola stavebních detailů, analýza tepelných mostů. Termografii je však možné také využít při určení součinitele prostupu tepla obálky budovy.
1 Úvod
Termografie je dnes zcela běžně využívána pro diagnostikování kvality obálky budov. Hlavním cílem je obvykle kontrola stavebních detailů, analýza tepelných mostů. Termografii je však možné také využít při určení součinitele prostupu tepla obálky budovy. Tato metoda určení součinitele prostupu tepla má však jistá omezení a vždy nemusí podat přesné výsledky. Důvodem je proměnlivost okrajových podmínek a též možná nehomogenita stavební konstrukce. Článek popisuje teoretickou metodu určení součinitele prostupu tepla na základě využití termografie. Na základě probíhajících výzkumů bude později publikován navazující článek, ve kterém bude provedena validace uvedené metodiky a její zhodnocení využitelnosti pro praxi.
2 Užití termografie k určení součinitele prostupu tepla
Známe-li teplotu uvnitř místnosti ti, teplotu v exteriéru te, teplotu povrchu konstrukce tp a součinitel přestupu tepla αe, jsme schopni určit součinitel prostupu tepla U. Vycházíme z rovnice tepelného toku:
kde
- Q
- – tepelný tok [W],
- U
- – součinitel prostupu tepla [W.m−2.K−1],
- S
- – plocha povrchu [m2],
- ti
- – teplota vzduchu v interiéru [°C],
- te
- – teplota vzduchu v exteriéru [°C].
Dále platí rovnice pro přenos tepla z povrchu konstrukce:
kde
- αe
- – součinitel přestupu tepla na straně exteriéru [W.m−2.K−1],
- tpe
- – teplota povrchu konstrukce na straně exteriéru [°C].
Na základě rovnosti teplených toků platí z rovnic (1) a (2):
Následně lze vyjádřit rovnici pro výpočet součinitele prostupu tepla:
V rovnici (4) lze aplikovat místo povrchové teploty vnější strany konstrukce povrchovou teplotu vnitřní strany konstrukce, podrobnosti např. zde [1].
2.1 Určení součinitele přestupu tepla – složka radiační
Klíčovou veličinou ve vztahu (4) je součinitele přestupu tepla αe, který má zásadní vliv na výsledek výpočtu a jeho stanovení je komplikovanou záležitostí. Součinitel je tvořen dvěmi složkami, a to konvekční αr a radiační αk.
Součinitel přestupu tepla radiací je možné stanovit několika způsoby, zjednodušeně např. dle normových požadavků [2]. Přesněji s pomocí následující rovnice:
kde

- – hustota měrného tepelného toku radiací [W.m−2].
Hustota tepelného toku radiací na externí straně obvodové stěny se skládá z vlastního radiačního toku a radiačního toku odraženého z okolního prostředí [3]. Při jeho výpočtu lze postupovat následovně:
kde
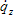
- – hustota vlastního měrného tepelného toku radiací [W.m−2],
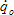
- – hustota vlastního měrného tepelného toku radiací okolního prostředí [W.m−2].
Dále platí následující rovnice:
kde
- ε
- – emisivita povrchu [-],
- σo
- – Stefanova-Boltzmannova konstanta, σo = 5,6697.10−8 [W.m−2.K−4]
- Tpe
- – termodynamická teplota povrchu konstrukce na straně exteriéru [K].
Hustotu vlastního měrného tepelného toku radiací okolního prostředí lze vyjádřit následně takto:
kde
- Tr
- – radiační teplota [K].
2.2 Určení součinitele přestupu tepla – složka konvekční
Pro součinitel přestupu při volném proudění podél svislé konstrukce v neohraničeném prostoru platí rovnice [4]:
kde
- Nu
- – Nusseltovo číslo [-],
- λ
- – součinitel tepelné vodivosti [W.m−1.K−1],
- h
- – charakteristický rozměr [m].
Nusseltovo číslo je možné stanovit z rovnice:
kde
- C, n
- – konstanty stanové experimentálně [-],
- Gr
- – Grasshoffovo číslo [-],
- Pr
- – Prandtlovo číslo [-].
Grasshoffovo číslo je možné vypočítat ze vztahu:
kde
- β
- – součinitel teplotní roztažnosti [K−1],
- g
- – tíhové zrychlení [m.s−2],
- h
- – charakteristický rozměr [m],
- Δt
- – rozdíl teploty vzduchu a povrchu konstrukce [K],
- ν
- – kinematická viskozita [m2.s−1].
Prandlovo číslo lze vypočítat pomocí vztahu níže:
kde
- a
- – teplotní vodivost [m2.s−1].
Konstanty C a n ze vztahu (11) závisí na druhu a intenzitě proudění. V souvislosti s tepelnou technikou se používají hodnoty C = 0,135 a n = 1/3. Dosadí-li se tyto hodnoty do vztahu (11) a také hodnoty příslušných veličin do Nusseltova, Grasshoffova a Prandtlova čísla, může se vyjádřit součinitel přestupu tepla v tomto tvaru [5]:
Ve vztahu (14) číselná hodnota K = 1,73 představuje souhrn všech číselných hodnot dosazených do vztahu (11) při určující teplotě tur = 0 °C. Jestliže je určující teplota tur ≠ 0 °C, mají fyzikální veličiny dosazované do podobnostních čísel Nu, Gr, Pr jiné hodnoty, takže i jejich souhrnná hodnota K bude jiná než 1,73. Tato hodnota K se zjistí, v závislosti na určující teplotě tur, z tab. 1.
| tur [°C] | −30 | −20 | −10 | 0 | 10 | 20 | 30 | 50 |
| K [–] | 1,87 | 1,82 | 1,77 | 1,73 | 1,68 | 1,64 | 1,61 | 1,54 |
Určující teplota tur se stanovuje jako aritmetický průměr teploty na povrchu konstrukce a teploty vzduchu:
3 Závěr
Výpočet součinitele prostupu tepla s využitím termografie je náročný, jak je doloženo výše v článku. Je nutné si uvědomit, že výpočet může být zatížený velkou chybou vzhledem k množství veličin, které vstupují do výpočtu. Vztah (4) lze modifikovat tak, aby výpočet byl proveden na základě teplot na vnitřní straně konstrukce, viz [1]. V tomto případě se vychází z teplot povrchů získaných měření příložným teploměrem. V praxi se běžně neurčuje součinitel prostupu tepla za pomocí termogramu z výše uvedených důvodů. Je možné se setkat s touto činností při výzkumné a experimentální činnosti na akademické půdě.
4 Poděkování
Tento článek byl napsán za přispění projektu „AdMas – Pokročilé stavební materiály, konstrukce a technologie“, registrovaným pod číslem CZ.1.05/2.1.00/03.0097 a financovaným MŠMT ČR.
5 Literatura
- [1] STRAKOVÁ, R., KNOB, J.: Měření součinitele prostupu tepla stávajících stavebních konstrukcí, Praha: Topinfo s.r.o., 2011. ISSN 1801-4399.
[http://stavba.tzb-info.cz/prostup-tepla-stavebni-konstrukci/8125-mereni-soucinitele-prostupu-tepla-stavajicich-stavebnich-konstrukci]. - [2] HORÁK, P.: Využití termovize při diagnostice tepelně-technického stavu obálky budov, příspěvek na konferenci Mezinárodní konference Progress 2012, Ostrava, 2012.
- [3] PAVELEK, M. a kol.: Termomechanika, skripta, Brno: VUT FSI, 2003.
- [4] GEBAUER, G.: Termika pro TZB, skripta, Brno: VUT FAST, 1996. ISBN 80-214-0745-X.
- [5] Řehánek, J.: Tepelná akumulace budov, ČKAIT Praha, 2002. ISBN 80-86364-59-3.
V článku autoři podrobně rozebírají možnost výpočtu součinitele prostupu tepla na základě údajů získaných termovizním měřením. Je zřejmé, že výpočet je komplikovaný, ale možný. Domnívám se, že najde uplatnění zejména při výzkumné činnosti.
Currently the thermography is commonly used for diagnosis of the building envelope quality. Major purpose is the control of construction details, thermal bridge analysis. Thermography can be used for determining the heat transfer coefficient of the building envelope. Though this method of determining heat transfer coefficient is limited and results may not always be exact. It can be caused by variability of boundary conditions and inhomogeneity of building structure. This article describes the methodology for determination of heat transfer coefficient based on thermographic measuring.