Dynamické chování otopných těles s ohledem na regulační zásah
V ideálním případě požadujeme, aby se tepelné ztráty rovnaly aktuálně dodávanému tepelnému výkonu. Tento proces je však v čase nestálý a prostřednictvím procesů regulace tepelného výkonu se snažíme co nejpřesněji reagovat na dané změny podmínek. Abychom dosáhli co nejefektivnější regulace, je třeba zabývat se dynamickým chováním otopných ploch obecně. Zde rozumíme dynamickým chováním reakci na vyvolaný regulační zásah. Příspěvek se zabývá dynamickým chováním otopného tělesa s místní kvantitativní regulací přes termostatický regulační ventil opatřený hlavicí s kapalinovou náplní (dále jen „TRV“).
Úvod do problematiky
Typickým představitelem dynamického děje je náběh či chladnutí otopného tělesa. Pro jejich posouzení je třeba sledovat charakteristické veličiny, jakými jsou například tepelný výkon nebo střední povrchová teplota otopného tělesa. Vyhodnocení takových dějů je nejčastěji vyjádřeno v grafické podobě. Z pohledu regulace jsou získané křivky přechodovými charakteristikami, tedy odezvami výstupní veličiny na skokovou změnu veličiny vstupní, a jelikož si v technice prostředí mnohdy vystačíme právě se skokovou změnou vstupů, zabývali jsme se především nespojitým (dvoupolohovým) chováním TRV.
Dynamické vlastnosti otopných těles
Setrvačnost náběhu a chladnutí
Setrvačnost náběhu resp. chladnutí je vedle jiných, základním provozním parametrem otopných ploch. Určujeme hodnoty Tn63 a Tn90, což jsou doby potřebné k dosažení 63,2 resp. 90% jmenovitého tepelného výkonu otopné plochy. T63 a T90 pak slouží jako porovnávací kritéria dynamického chování pro různé druhy otopných ploch a to jak pro náběh, tak pro chladnutí. Tyto hodnoty zjišťujeme spolehlivě zatím pouze měřením [4].
Chladnutí otopných těles
Jedná se o snižování střední povrchové teploty otopného tělesa v důsledku ztrátového tepelného toku z povrchu tělesa. V případě ochlazování uvažujeme, že tepelný tok směrem do tělesa je nulový (TRV uzavřen). Jednotlivé tepelné toky můžeme vyjádřit ze základní tepelné bilance akumulace = přívod − odvod [3]. Po úpravách uvedených v [3] získáme rovnici popisující teoretický průběh (přechodovou charakteristiku) chladnutí otopného tělesa. Grafické vyjádření tohoto vztahu je například v [1]. Jedná se o exponenciálně závislou křivku prvního řádu probíhající mezi dvěma ustálenými stavy. Nalezneme zde jediný parametr popisující dynamické chování, který zároveň udává rychlost celého přechodového jevu a je jím časová konstanta τ0. Tuto definujeme jako dobu potřebnou k dosažení 63,2% poklesu z celého přechodového děje (dosažení inflexního bodu). V souladu s výše uvedeným je τ0 = T63 hlavním porovnávacím kritériem.
Náběh otopných těles
Analogickým způsobem jako u chladnutí vycházíme ze základní tepelné bilance a dojdeme k obdobnému řešení, opět popisujícímu křivku s parametrem τ0. V aplikacích techniky prostředí se však nejčastěji setkáváme s přechodovými charakteristikami druhého a vyšších řádů a právě náběhová křivka je jedním z takových případů. Křivky druhého řádu mohou obsahovat dobu průtahu či dopravní zpoždění. S těmito aspekty je nutno při hlubším řešení dynamiky kalkulovat. Pro naše vyhodnocení výsledků měření jsou tyto veličiny zanedbány [2].
Měření a vyhodnocení
V laboratořích Ústavu techniky prostředí FS ČVUT v Praze bylo postupně napojováno několik druhů a typů otopných těles k měřicí soustavě [1] několika způsoby připojení, z nichž alespoň jeden byl vždy jmenovitý. Proces náběhu a chladnutí byl pak sledován termovizní kamerou.
Měření náběhu vyžaduje především stav, kdy je otopné těleso na počátku měření teplotně vyrovnané se svým okolím tzn., že střední povrchová teplota tělesa se rovná teplotě okolního vzduchu. Naopak pro měření chladnutí je nezbytné vycházet ze stavu, kdy má otopné těleso jmenovité teplotní parametry. Protože doba chladnutí je podstatně delší, odpovídají tomu i delší intervaly snímaní povrchových teplot.
Stanovení hodnot setrvačnosti náběhu a chladnutí
Záznamem termovizní kamery vlastně sledujeme závislost střední povrchové teploty tělesa na čase (tp = f (τ)), díky čemuž získáme grafické vyjádření dynamického procesu, tedy křivku náběhu resp. chladnutí. Sledovat tp umožňuje fakt, že přestup tepla na straně vody je daleko intenzivnější než přestup tepla na straně vzduchu a zároveň součinitel tepelné vodivosti tenkého materiálu tělesa je vysoký. Za těchto předpokladů můžeme konstatovat, že střední teplota teplonosné látky twm se přibližně rovná tp. Postupem uvedeným v [1] převedeme závislost tp = f(τ) na závislost poměrného tepelného výkonu otopného tělesa na čase Q/QN = f(τ). Podle tohoto vztahu již snadno nalezneme hodnoty T63 a T90 náběhu i chladnutí (T63⇔Q/QN = 0,632; T90⇔Q/QN = 0,9). Grafické výstupy pro jednotlivé druhy a typy otopných těles v kombinaci s různými způsoby připojení jsou velice rozsáhlé [1], proto zde uvádíme pouze výslednou tabulku, zachycující zkorigované hodnoty setrvačnosti náběhu a chladnutí, tak abychom je mohli porovnávat.
| Druh a typ otopného tělesa | Způsob připojení | Setrvačnost náběhu [min] | Setrvačnost chladnutí [min] | ||
|---|---|---|---|---|---|
| Tn63 | Tn90 | Tch63 | Tch90 | ||
| Desková | |||||
| KL 10 – 500 × 500 | jednostr. shora dolů | 4,3 | 6,4 | 18 | 43 |
| oboustr. shora dolů | 4,3 | 6,8 | 18,5 | 43,9 | |
| KL 10 – 500 × 1000 | jednostr. shora dolů | 3,7 | 5,4 | 17,9 | 42 |
| oboustr. shora dolů | 3,8 | 5,8 | 18,1 | 43,3 | |
| KL 10 – 500 × 2000 | jednostr. shora dolů | 3,6 | 5,4 | 18,7 | 44,9 |
| oboustr. shora dolů | 3,5 | 5,2 | 18,1 | 42,1 | |
| Článková | |||||
| Kalor 10 / 500 / 70 | jednostr. shora dolů | 7,9 | 11,7 | 43,5 | 102,7 |
| oboustr. shora dolů | 8,3 | 12,3 | 40 | 93,7 | |
| Kalor 10 / 500 / 220 | jednostr. shora dolů | 7,8 | 12,3 | 45,3 | 109 |
| oboustr. shora dolů | 8,1 | 12,3 | 43,9 | 106,4 | |
| Trubková | |||||
| KLC – 1200 × 600 | oboustr. zdola dolů | 8,6 | 18,1 | 28,5 | 60,3 |
Je zde zřetelný rozdíl hodnot T63 mezi jednotlivými tělesy. V rámci jednoho druhu těles jsou hodnoty srovnatelné, ale v porovnání s jinými druhy se hodnoty výrazně liší. Např. článková litinová otopná tělesa dosahují cca dvojnásobných hodnot než desková. Je to dáno především daleko vyšší tepelnou kapacitou článkových litinových těles (silnostěnný materiál a větší vodní objem). Trubkové těleso se bude svým dynamickým chováním blížit spíše tělesům článkovým. Všechny tyto aspekty samozřejmě výrazně ovlivňují dynamické chování daného otopného tělesa.
Simulace dynamického chování otopného tělesa
Způsob regulace
Posuzujeme především místní dvoupolohovou kvantitativní regulaci. Jedná se tedy o regulaci, kdy měníme pouze hmotnostní průtok teplonosné látky, přičemž její teplota zůstává konstantní. Všechny výše uvedené parametry dokážeme zajistit prostřednictvím TRV, který je typickým zástupcem P-regulátoru, tedy spojitého proporcionálního regulátoru s nastaveným pásmem proporcionality. Toto platí, pokud je termostatický ventil osazen servo či termopohonem. V praxi však většinou bývá osazen jednoduchou kapalinovou či paroplynovou hlavicí a v této kombinaci se skutečně regulační průběh blíží dvoupolohovému chování (otevřeno/zavřeno) [2]. Samotná simulace průběhu dynamického chování pak spočívá ve skládání dříve získaných křivek náběhu a chladnutí okolo požadované hodnoty v rámci stanoveného pásma proporcionality.
Pásmo proporcionality
Pro simulaci jsme zvolili celkem tři pásma proporcionality, a to 1, 2 a 3 K okolo požadované teploty 20 °C (tzn. 20 ± 0,5 K; 20 ± 1 K; 20 ± 1,5 K). Správná volba pásma proporcionality TRV má na jeho provozní chování zásadní vliv. Pokud bude ventil poddimenzován, bude pracovat ve stále otevřené poloze a nebude plnit svoji regulační funkci. Ve výsledku pak nebude otopné těleso podávat tak vysoké výkony, jaké očekáváme. Naopak předimenzovaný TRV pracuje v poloze téměř zavřeno a opět neplní svou regulační funkci. Ventil neustále zavírá a otevírá, což může vést k jeho nadměrnému opotřebení či hlukovým projevům. Pokud volíme pásmo užší např. ± 0,5 K, můžeme dosáhnout přesnější regulace konečné hodnoty, obnáší to ovšem podobný problém jako předimenzovaný TRV, tzn. nestabilitu a ztrátu regulační schopnosti. Při volbě širšího pásma proporcionality pak snižujeme nároky na dosažení žádaných úspor energie. Teplotní rozsahy byly převedeny na rozsahy výkonové (tak aby korelovaly se získanými průběhy křivek), resp. stanovili jsme horní x2 a dolní x1 spínací hodnoty.
Ke sledování dynamického chování bylo vybráno deskové otopné těleso KL 10 – 500 × 1000 s připojením oboustranně shora dolů. Simulovány byly celkem tři provozní stavy. Nejprve stav kdy je potřeba 100 % výkonu tělesa, dále stav kdy je zapotřebí 62,6 % a 10 % výkonu otopného tělesa tak, abychom měli představu o chování regulátoru v celém výkonovém spektru.
Vyhodnocení
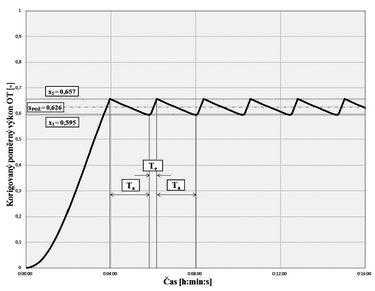
Obdobně jako v předešlém odstavci, tak i zde je velké množství vyhodnocených průběhů [1]. Proto byl vybrán průběh dynamického chování (reakce na regulační zásah) pouze výše uvedeného tělesa pro 62,6% potřebu výkonu a pro pásmo proporcionality 20 ± 1 K (obr. 1).
Z obr. 1 je zřejmé, že na počátku je regulovaná veličina rovna 0 %. Jelikož je požadovaná hodnota xpož = 62,6 %, vzniká zde regulační odchylka, na kterou reaguje regulátor tak, že zapíná svou akční veličinu (vlnovec se uvolňuje a pružina zvedá kuželku). Tímto zvýší průtok teplonosné látky otopným tělesem, což způsobí nárůst střední povrchové teploty otopného tělesa, resp. jeho výkonu. Náběh probíhá u jednotlivých otopných těles podle získané křivky náběhu s časovou konstantou τ0 resp. T63, a to až do okamžiku, kdy je dosaženo horní spínací hodnoty x2. Pokud ve vytápěném prostoru dojde ke změně požadavku ve smyslu snížení požadované teploty nebo je dosaženo právě hodnoty x2, dvoupolohový regulátor zavírá ventil a otopné těleso začíná chladnout podle získané křivky chladnutí. Toto probíhá do chvíle, kdy je dosaženo spodní spínací hodnoty x1. Následně je ventil opět otevřen a těleso nabíhá k hodnotě x2. Po prvotním náběhu, kdy je dosaženo spínací hodnoty x2, dochází k cyklování průběhu tepelného výkonu v rámci rozmezí hodnot x1 a x2. Dobu, po kterou otopné těleso chladne, nazýváme dobou vypnutí Ta a dobu, po kterou se výkon pohybuje po náběhové křivce, nazýváme dobou zapnutí Te [4]. Právě tyto dvě hodnoty, resp. jejich poměr byl využit jako porovnávací kritérium (viz tab. 2). V praxi dochází ještě k překmitu požadovaného rozsahu a ten se pak rozšiřuje do tzv. pásma kolísání. Zde je však překmitnutí zanedbáno.
| Potřeba výkonu | Pásmo proporcionality | Doba zapnutí | Doba vypnutí | Poměr Ta / Te [-] |
|---|---|---|---|---|
| Te [min] | ||||
| 100 % | ± 0,5 K | 4,42 | 0,42 | 0,1 |
| ± 1 K | 5,33 | 0,67 | 0,13 | |
| ± 1,5 K | 5,92 | 0,92 | 0,16 | |
| 62,6 % | ± 0,5 K | 0,2 | 1 | 5 |
| ± 1 K | 0,35 | 1,87 | 5,34 | |
| ± 1,5 K | 0,53 | 2,88 | 5,43 | |
| 10 % | ± 0,5 K | 0,23 | 6,08 | 26,43 |
| ± 1 K | 0,42 | 11,68 | 27,81 | |
| ± 1,5 K | 0,65 | 18,38 | 28,28 | |
Závěr
100% potřeba výkonu je stav specifický tím, že střední, tedy požadovaná hodnota xpož je rovna horní spínací hodnotě x2. Máme tedy k dispozici pouze polovinu spínacího rozsahu. Oproti ostatním průběhům je tento stav specifický tím, že doba zapnutí je výrazně delší než doba vypnutí. Toto je dáno úseky křivek, ve kterých se s rozsahem pohybujeme. Náběhová křivka je v tomto rozmezí velice plochá, naopak křivka chladnutí je ve své nejstrmější části. Z tohoto důvodu je poměr doby vypnutí a doby zapnutí Ta / Te menší než jedna. V praxi však výše zmíněné nebude zcela platit, neboť výkony otopných těles nejsou navrženy přesně na jmenovitou tepelnou ztrátu, ale díky dané výrobní řadě těles mohou mít vyšší výkon, než je jmenovitá tepelná ztráta. Většinou tak projektant předimenzuje otopná tělesa o 5 až 15 % vůči skutečné tepelné ztrátě místnosti. Značí to tedy, že budeme ve skutečnosti mít i za jmenovitých podmínek k dispozici celý spínací rozsah. Pro všechny sledované průběhy také platí, že v nejužším pásmu proporcionality (± 0,5 K) je počet cyklů vyšší než v širších sledovaných pásmech. Tento závěr je tedy ve shodě s výše popsaným faktem, že užší spínací diference zapříčiní větší kmitání kuželky ventilu a způsobuje vyšší opotřebení či hlukové projevy.
Pro 62,6% potřebu výkonu již pozorujeme jak dolní, tak horní spínací hodnotu, a tudíž jsou sledované rozsahy dvojnásobně širší než u 100% teoretické potřeby výkonu. Přesto, že je pásmo širší, není rozdíl mezi dobou zapnutí a vypnutí tak markantní jako u předchozího stavu. Zde je doba vypnutí delší než doba zapnutí, což je opět dáno průběhem jednotlivých křivek. Chladnutí má v tomto rozsahu výrazně plošší průběh než náběh. Tím je dáno, že počet cyklů za srovnatelné časové rozmezí je v tomto případě vyšší a jednotlivé cykly jsou tudíž kratší.
Při 10% potřebě výkonu se nacházíme na opačné straně výkonového spektra a to znamená, že křivka náběhu je ve své téměř nejstrmější části a křivka chladnutí je skoro plochá. Proto poměr dob vypnutí a zapnutí vychází nejvyšší právě zde. Rozdíl v počtu cyklů mezi ± 0,5 K a ± 1,5 K je téměř dvojnásobný a zde se tedy velmi názorně ukazuje praktický rozdíl v návrhu regulátoru pro zajištění jeho správné funkce a dlouhodobé spolehlivosti.
Z výše uvedeného je patrné, jak důležitá je znalost setrvačnosti náběhu a chladnutí u otopných těles resp. průběhů křivek. Chování regulátorů je jiné v různých částech výkonového spektra. Do rychlosti odezvy se promítá i akumulace otopných těles, resp. jejich tepelná setrvačnost. Samotná reakce otopných těles na regulační zásah je proto prodloužena o dobu úměrnou tepelné setrvačnosti.
Všechny uvedené průběhy byly určeny pouze pro jednu požadovanou hodnotu. Reálně se však potřeba tepla neustále mění, např. vlivem oslunění, změnou požadavků nebo díky vnitřním zdrojům tepla apod. Tomuto rozboru se dále věnuje [1].
Použité zdroje
- [1] Boháč J. Diplomová práce Dynamické chování otopných těles. Praha: ČVUT, 2012. 136 s.
- [2] Bašta J. Regulace vytápění. Praha: Nakladatelství ČVUT, 2007. 99 s. ISBN 978–80–01–02582–6.
- [3] Šimek J. Diplomová práce Dynamické chování otopných těles. Praha: ČVUT, 2007. 110 s.
- [4] Bašta J. Hydraulika a řízení otopných soustav. Praha: Nakladatelství ČVUT, 2003. 252 s. ISBN 80–01–02808–9.
We require that heat losses be equal to the currently supplied heat output, in an ideal event. However, this process is unsettled in time and we try to react precisely as best to the given changes of conditions through processes of the heat output control. It is necessary to deal with the dynamic behavior of heating surfaces, generally, to be able to achieve the most efficient control. The dynamic behavior is understood herein as the reaction towards the invoked control intervention. Authors are engaged in the dynamic behavior of radiators with local quantitative control through the thermal control valve fitted with the head with the liquid charge (hereinafter the “TRV” – Thermostatic Radiator Valve), in their contribution.